تعیین جمله های طیفی به روش فاکتور گیری از اسپین
این روش با مقایسه با روش راسل ـ ساندرز به نسبت ساده است. در این روش «ترمـهای جزئی»
برای هر مجموعه ای از اسپین هاست. با ضرب کردن ترم های جزئی مربوط به مجموعه اسپینها
در یکدیگر که با نشانه های α برای m[SUB]s [/SUB]= +1/2 و β برای m[SUB]s [/SUB]= - 1/2 مشخص می شوند، جمله
های طیفی کلی را می توان بدست آورد.
در تعیین ترم های جزئی باید نکته های زیر را مورد توجه قرار داد:
* تراز های الکترونی خالی، نیم پر یا به طور کامل پر، سهمی در اندازه حرکت زاویه ای اوربیتالی
ندارند و به ترم جزئی S تعلق دارند. در نتیجه یک مجموعه اسپین خالی یا یک مجموعه اسپین کامل
(تراز نیم پر) نیز به همین ترم جزئی S تعلق دارد.
* یک الکترون در هر تراز انرژیی که هست دارای ترم جزئی با همان نشانه طیفی آن تراز است. یعنی
ترم جزئی یک الکترون در تراز p با P و ترم جزئی یک الکترون در تراز d با D و... مشخص می شود.
بنابراین، هر مجموعه اسپین (α یا β) که شامل یک الکترون است، به همین ترم های جزئی مربوط
است.
* هر جای خالی از یک مجموعه اسپین (یک حفره الکترونی) به همان جمله جزئی که یک الکترون
در آن مجموعه می دهد تعلق دارد. برای مثال برای آرایش الکترونی p[SUP]1[/SUP][SUB]α[/SUB] یا p[SUP]2[/SUP][SUB]α[/SUB] ترم جزئی P ، برای
آرایش الکترونی d[SUP]1[/SUP][SUB]α[/SUB] یا d[SUP]4[/SUP][SUB]α[/SUB] ترم جزئی D ، و برای آرایش الکترونی f[SUP] 1[/SUP][SUB]α[/SUB] یا f [SUP]6[/SUP][SUB]α[/SUB] ترم جزئی F را خواهیم
داشت. جمله های جزئی مربوط به یک مجموعه اسپین آرایش الکترونی متفاوت در جدول زیر نشان
داده شده است.
* اگر آرایش الکترونی d[SUP]2[/SUP][SUB]α[/SUB] را در نظر بگیریم، 10 حالت ریز برای آن می توان به دست آورد، که مقدار
های M[SUB]L[/SUB] آن ها عبارتند از:
-3 ,-2 ,-1 , 0 , 1 , 2 , 3 ؛ -1 , 0 , 1 و در نتیجه به ترم های جزئی F و P تعلق دارند که در جدول
زیر برای آرایش الکترونی d[SUP]2[/SUP] منظور شده است. چون آرایش الکترونی d[SUP]3[/SUP][SUB]α[/SUB] هم ارز آرایش حفره d[SUP]2[/SUP][SUB]α[/SUB]
است، پس ترم های جزئی d[SUP]3[/SUP][SUB]α[/SUB] نیز F و P است. در مورد آرایش های الکترونی دیگر نیز می توان به
همین روش عمل کرد.
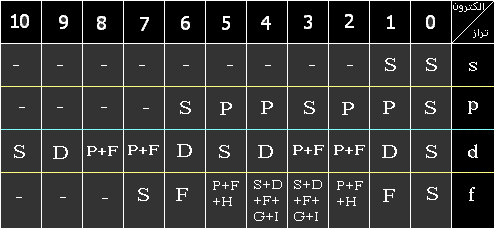
* کافی است که ترم های جزئی سمت چپ خط وسط جدول را به دست آورد. ترم های سمت راست
آن را بر اساس فرمالیسم حفره، می توان با قرینه معین کرد.
برای استفاده از ترم های جزئی و به دست آوردن جمله های طیفی باید، حاصلضرب ترم های جزئی در
یکدیگر را بدانیم.
حاصلضرب ترم های جزئی
از ضرب ترم جزئی S در هر ترم جزئی دیگر، همان ترم جزئی به دست می آید. یعنی:
S × S = S
S × P = P
S × D = D
S × F = F
باید توجه داشت که حاصلضرب دو ترم جزئی با مقدار های L[SUB]1[/SUB] و L[SUB]2[/SUB] ، شامل ترم هایی خواهد بود که تمام
مقدار های درست از L[SUB]1[/SUB] + L[SUB]2[/SUB] تا |L[SUB]1[/SUB] – L[SUB]2[/SUB]| را در بر دارد.
برای مثال در مورد ترم های P و D ، چون L مربوط به ترم P برابر 1 و L مربوط به ترم D برابر 2 است، بنابراین،
L شامل مقدار های درست از 2+1 تا 2-1 یعنی: 3 , 2 , 1 خواهد بود. از این رو می توان نوشت:
P × D = P + D + F
بر همین اساس، در مورد حاصلضرب ترم های دیگر خواهیم داشت:
P × P = S + P + D
P × F = D + F + G
D × D = S + P + D + F + G
D × F = P + D + F + G + H
