تقارن در شیمی معدنی

[S H i M A]

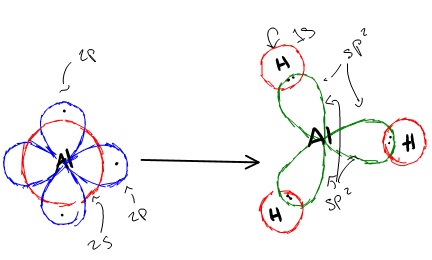
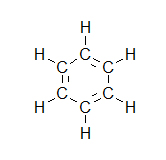
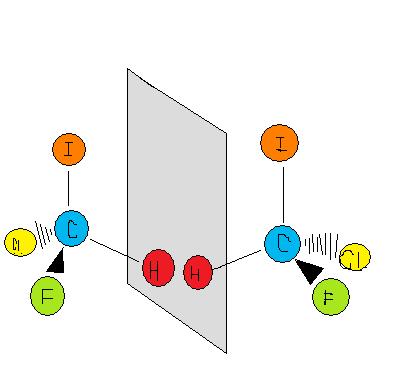
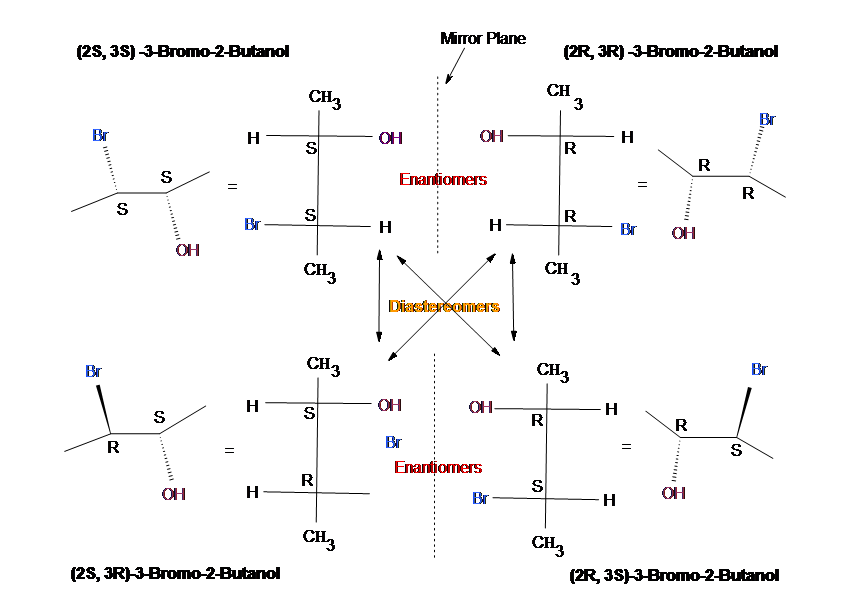
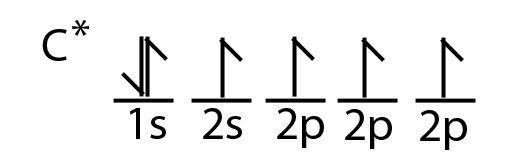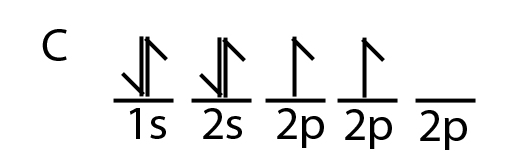تقارن در شيمي زمينه حل بسياري از مسائل علم شيمي مانند: ساختار ملكول.ساختار الكترون.

تشكيل پيوند و هيبريداسيون همچنين پيش بيني طيف زير قرمز را فراهم ميكند.

در اينجا به بررسي تقارن ملكولهاي مجزا ميپردازيم كه تقارن آنها به تقارن نقطه اي موسوم است.


مفاهيم مهم در تقارن

1-عنصر تقارن: واقعيتي هندسي مانند خط صفحه و يا نقطه كه يك يا چند عمل تقارن نسبت به

آن انجام ميشود.

2-عمل تقارن: حركت يا عملي كه انجام آن روي ملكول يا سيستم وضعيت جديدي ايجاد كند طوري

كه وضعيت جديد از وضعيت قبلي ملكول يا سيستم غير قابل تمييز باشد.

پس وضعيت جديد شبيه به وضعيت قبليست اما معادل با آن نيست.

در تقارن اين دو مفهوم به نحو جدايي ناپذيري به هم مربوط اند.چون عمل تقارني فقط به پشتوانه يك

عنصر تقارن انجام ميشود و به همين ترتيب وجود عنصر تقارن تنها زماني براي سيستم اهميت دارد

كه بتوان روي آن يك عمل تقارني انجام داد.


5 نوع عنصر تقارن و عمل تقارني براي مشخص كردن تقارن ملكولي:

1- عنصر يكسانيE

2-محور چرخشي Cn

3-مركز وارونگي يا مركز تقارن i

4-صفحه تقارن يا صفحه آيينه اي σ

5-محور چرخشي-انعكاسي Sn


1- عنصر يكساني E

عمل يكساني هيچ تغييري در ملكول ايجاد نميكند و شامل چرخش ملكول به اندازه360درجه است.

پس هر شيء يا سيستمي داراي عمل يكساني E است.

این عمل ، هیچ تغییری در مولکول ایجاد نمی‌کند. هر مولکولی ، یک عمل یکسانی دارد، حتی اگر

هیچ تقارنی نداشته باشد.

نتيجه عمل يكساني روي نقطه اي به مختصات x y z را به صورت زير نشان ميدهند.


x1.y1.z1---------->x1.y1.z1



2- محور چرخشي

محور چرخشي متعارف به صورت Cnنشان داده ميشود و nمرتبه محور دوران است كه محوري است

فرضي و عمل تقارني چرخش به اندازهn/360 حول آن محور بطوريكه ملكول به حالتي مشابه حالت

اوليه اش باز گردد را موجب ميشود.

عمل چرخشی که چرخش متعارف نیز نامیده می‌شود، مستلزم چرخش به اندازه 360 بر n درجه

حول محور چرخش است.

به طور مثال C2 و C3 و C4 به ترتيب نشان دهنده دوران به اندازه 180 و 120 و 90 درجه است.

C1:

محور چرخشي C1 ملكول و اتم ها را به اندازه 360 درجه ميچرخاند پس معادل با عمل E ميباشد.

پس هر سيستمي داراي محور C1 است حتي محل قرار گرفتن آن مهم نيست چرا كه اين محور

را هر جادر نظر بگيريم و سيستم را نسبت به آن و با زاويه 360 درجه بچرخانيم به حالت اوليه باز

ميگردد.

C2:

براي استفاده از محور c2 بايد اتم مركزي حداقل دو ليگند داشته باشد تا با زاويه180درجه بچرخند.

مثال- ملكول آب را در نظر بگيريد.اين ملكول كاملا در صفحه دو بعدي قرار دارد پس محور آن هم در

همان صفحه تعريف خواهد شد.

با چرخش سيستم تحت c2 سيستم وضعيتي مشابه وضعيت قبل پيدا كرده اما با آن معادل نيست

چراكه مشاهده ميشود كه جاي اتم h1 و h2 باهم عوض شده.

توان گذاشته شده براي c تعداد دفعات اعمال c2 روي سيستم را مشخص ميكند.بنابراين توان دو

به اين معنيست كه چرخش سيستم به اندازه 180 درجه تحتc2 دو بار انجام شده كه سيستم را

به حالت اوليه بازميگرداند.


اگر محور فرضي C2 منطبق بر محور Z باشد هر نقطه اي به مختصاتx y z به صورت زير تغيير ميكند:

XYZ------->-X -Y Z

و اگر اين محور منطبق بر محور X باشد آنگاه خواهيم داشت:

X Y Z-------->X -Y -Z


CHCl[SUB]3[/SUB] نمونه ای از مولکولهایی است که دارای محور درجه سه (C[SUB]3[/SUB]) می‌باشند و در آن ، محور چرخش

بر محور پیوند C-H منطبق است. اگر چرخش C[SUB]3[/SUB] دوبار پشت سرهم انجام می‌گیرد، یک چرخش جدید

˚240حاصل می‌شود که با C[SUP]2[/SUP][SUB]3[/SUB] نشان داده شده و جزو اعمال تنقارن مولکولی نیز می‌باشد.

سه عمل متوالی C[SUB]3[/SUB] برابر عمل یکسانی است (C[SUP]3[/SUP][SUB]3[/SUB]=E) که در همه مولکولها وجود دارد.

بسیاری از مولکولها و اجسام دیگر محورهای چرخش متعددی دارند.


ملكول BF3 را در نظر بگيريد.

داراي محور چرخشي مرتبه 3 ميباشد.در اين ملكول محور تقارنC3 عمود بر صفحه كاغذ است.اين

محور از اتم بور عبور ميكند و باعث چرخش ملكول به اندازه120درجه در جهت حركت عقربه هاي

ساعت ميشود.

ساختار اول مشابه ساختارهاي دوم و سوم است و معادل با ساختار آخر.

بنابر اين ميتوان نتيجه گرفت هر Cn به توان n و به عبارت ديگر هرمحور چرخشي با مرتبه n اگر n

مرتبه روي سيستم اعمال شود عملي معادل عنصر يكساني E دارد.

در مثال هاي قبل اين واقعيت مشهود است.

براي مشخص كردن جهت محورهاي مختصات محوري كه بالا ترين مرتبه را دارد محور اصلي منطبق

بر محور Z در نظر گرفته ميشود و بيشترين درجه چرخش كوچك ترين زاويه را دارا خواهد بود.

علاوه بر محور هاي مرتبه 2 و مرتبه 3 ملكول هاي شناخته شده اي نيز وجود دارند كه از محور هاي

بالاتري برخوردارند و تا مرتبه 8 ادامه دارند.

دانه‌های برف ، نمونه‌هایی در این مورد هستند، با شکلهای پیچیده ای که معمولا شش گوشه‌ای

تقریبا مسطح است. خطی که عمود بر صفحه دانه برف از مرکز آن گذشته ، دربرگیرنده یک محور درجه

دو (C[SUB]2[/SUB]) ، یک محور درجه سه (C[SUB]3[/SUB]) و یک محور درجه شش (C[SUB]6[/SUB]) است. دقت کنید که چرخش به اندازه

˚240 (C[SUP]2[/SUP][SUB]3[/SUB]) و ˚300 (C[SUP]5[/SUP][SUB]6[/SUB]) نیز جزو اعمال تقارن دانه برف می‌باشند.

همچنین دو مجموعه سه‌تایی دیگر از محورهای C[SUB]2[/SUB] در صفحه دانه برف وجود دارد که یک مجموعه از نقطه‌

های متقابل و مجموعه دیگر از وسط اضلاع میان نقطه‌ها می‌گذرد. در مولکولهای دارای بیش از یک محور

چرخشی ، محور C[SUB]n[/SUB] دارای بزرگترین مقدار n ممکن به‌عنوان محور چرخش با بزرگترین مرتبه یا محور اصلی

تعیین می‌شود.

محور چرخش با بزرگترین مرتبه در دانه برف ، محور C[SUB]6[/SUB] است. (در موقع انتقال به مشخصات کارتزین ، محور

C[SUB]n[/SUB] با بزرگترین مرتبه معمولا به‌عنوان محور Z انتخاب می‌شود). در صورت لزوم ، محورها C[SUB]2[/SUB] عمود بر محور

اصلی را با پریم مشخص می‌کنند. یک تک پریم نشان میدهد که محور از داخل چندین اتم مولکول میگذرد،

در حالی‌که یک جفت پریم نشان می‌دهد که محور از بین اتمها می‌گذرد.


3-مركز وارونگي يا مركز تقارن i

این عمل ، کمی پیچیده‌تر است. هر نقطه از وسط مرکز مولکول به موقعیتی مقابل موقعیت اولیه حرکت

می‌کند، به‌طوری‌که فاصله اش از نقطه مرکزی برابر با فاصله ای باشد که در آغاز داشت.

اتان در حالت صورتبندی نامتقابل نمونه ای از مولکولهایی است که دارای مرکز وارونگی می‌باشند. بسیاری

از مولکولها که در نگاه اول به نظر می‌رسد مرکز وارونگی دارند، فاقد آن هستند. متان و مولکولهای چهار

وجهی دیگر ، نمونه‌هایی از این مولکولها هستند.

اگر دو اتم هیدروژن یک مدل متان در صفحه عمودی سمت راست و دو اتم هیدروژن دیگرش در صفحه افقی

در چپ نگاه داشته شود، عمل وارونگی دو هیدروژن واقع در صفحه افقی را به سمت راست و دو هیدروژن

واقع در صفحه عمودی را به سمت چپ منتقل می‌کند. پس متان ، عمل وارونگی ندارد، چون جهت‌گیری

مولکول پس از عمل i با جهت‌گیری اولیه متفاوت است.

بطور کلی، چهار وجهی‌ها، مسطح مثلثی‌ها، پنج ضلعی‌ها مرکز وارونگی ندارند. مربعها، متوازی‌الاضلاعها،

اجسام راست‌گوشه و دانه‌های برف مرکز وارونگی دارند.


4-صفحه تقارن يا صفحه آيينه اي σ

عمل انعکاسی (σ) ، موقعی وجود دارد که مولکول ، دارای یک صفحه آینه‌ای باشد. اگر جزئیاتی نظیر آرایش

موها و محل اندامهای داخلی را در نظر نگیریم، بدن انسان دارای یک صفحه آینه‌‌ای چپ – راست می‌باشد.

بسیاری از مولکولها، صفحه آینه‌ای دارند، اگرچه ممکن است در نگاه اول آشکار نباشد.

عمل انعکاس، جای چپ و راست را عوض میکند، مانند اینکه هر نقطه بطور عمود از میان صفحه به موقعیتی

دقیقا در همان فاصله از صفحه که در آغاز بود، حرکت کرده است.

مولکولها می‌توانند به هر تعدادی صفحه آینه‌ای داشته باشند.

اجسام خطی نظیر یک مداد چوبی گرد یا مولکولهای همچون استیلن و کربن دی‌اکسید دارای تعداد نامحدودی

صفحه آینه‌ای هستند که همه آنها دربرگیرنده محور مرکزی جسم می‌باشند.


5-محور چرخشي-انعكاسي Sn

این عمل که گاهی اوقات ، چرخش نامتقارن نامیده می‌شود، مستلزم چرخش به اندازه 360 بر n درجه و به

دنبال آن ، انعکاس از صفحه عمود بر محور چرخش می‌باشد. برای مثال ، در متان ، خطی که از وسط کربن

عبور کرده و زاویه میان هیدروژنها را در طرفین نصف می‌کند، یک محور S[SUB]4[/SUB] می‌باشد. از این نوع خط سه تا و

در کل سه محور S[SUB]4[/SUB] وجود دارد.

این عمل ، مستلزم چرخش مولکول به اندازه ˚90 و سپس انعکاس از صفحه آینه‌ای عمود می‌باشد. دو عمل

متوالی S[SUB]n[/SUB] یک محور C[SUB]n[/SUB]/2 ایجاد می‌کند. در متان ، دو عمل S[SUB]4[/SUB] یک C[SUB]2[/SUB] ایجاد می‌کند.

بعضی وقتها ممکن است محور S[SUB]n[/SUB] مولکول با محور C[SUB]n[/SUB] آن منطبق باشد. مثلا دانه‌های برف ، علاوه بر محورهای

چرخش اشاره شده در بالا ، محورهای S[SUB]2[/SUB] ، S[SUB]3[/SUB] و S[SUB]6[/SUB] منطبق بر محور C[SUB]6[/SUB] نیز دارند.

دقت کنید که محور S[SUB]2[/SUB] با وارونگی و محور S[SUB]1[/SUB] با صفحه آینه‌ای یکسانی هستند. در مورد اول ، نماد i و در مورد

دوم نماد σ ترجیح داده می‌شود.

 

[S H i M A]

با دریافت کتاب زیر میتوانید انواع تقارن را از ابتدایی ترین تا پیچیده ترین مشاهده کنید:

دریافت



با کلیک بر روی لینک زیر میتوانید از سمت چپ، ترکیبات را انتخاب کرده و نحوه اعمال عناصر تقارن را ببینید:

ورود



همینطور با کلیک بر روی لینک زیر میتوانید خودتان روی عناصر تقارن کلیک کرده و نحوه چرخش را ببینید:

ورود

​

 

[S H i M A]

فلوچارت تقارن در شیمی:

​

 

[S H i M A]

معرفی دو کتاب مفید در زمینه نظریه گروه و تقارن در شیمی

کاربرد نظریه گروه و تقارن در شیمی - نوشته آلبرت کاتن

و نظریه گروه و شیمی - نوشته دیوید بی شاپ

دانلود


پسورد : alivechem.com


حجم : ۱۸٫۶۴MB
​

 

[S H i M A]

​

جدول های گروه های نقطه ای:

Character Tables of Symmetry Groups
​

Every molecule has a point group associated with it. The point groups are assigned by a set for rules (explained by Group theory). The character tables takes the point group and represents all of the symmetry that the molecule has



Symbols under the first column of the character tables

​

(A (Mulliken Symbol ​	(singly degenerate or one dimensional) symmetric with respect to rotation of the principle axis​
(B (Mulliken Symbol ​	(singly degenerate or one dimensional) anti-symmetric with respect to rotation of the principle axis​
(E (Mulliken Symbol ​	(doubly degenerate or two dimensional) (need to look up) ​
(T (Mulliken Symbol ​	(thirdly degenerate or three dimensional ) (need to look up)​
Subscript 1​	symmetric with respect to the C[SUB]n [/SUB]principle axis, if no perpendicular axis, then it is with respect to σ[SUB]v[/SUB]​
Subscript 2​	asymmetric with respect to the C[SUB]n [/SUB]principle axis, if no perpendicular axis, then it is with respect to σ[SUB]v[/SUB]​
Subscript g​	symmetric with respect to the inverse ​
subscript u​	asymmetric with respect to the inverse​
prime​	(asymmetric with respect to σ[SUB]h [/SUB](no reflection in horizontal plane ​
double prime​	(symmetric with respect to σ[SUB]h[/SUB] (reflection in horizontal plane ​

symbols in the first row of the character tables

​

E	(describes the degeneracy of the row (A and B= 1) (E=2) (T=3
C[SUB]n[/SUB]	(2pi/n= number of turns in one circle on the main axis without changing the look of a molecule (rotation of the molecule
C[SUB]n[/SUB]'	2π/n= number of turns in one circle perpendicular to the main axis, without changing the structure of the molecule
C[SUB]n[/SUB][SUP]"[/SUP]	2π/n= number of turns in one circle perpendicular to the C[SUB]n[/SUB]' and the main axis, without changing the structure
σ'	reflection of the molecule perpendicular to the other sigma
σ[SUB]v [/SUB](vertical)	reflection of the molecule vertically compared to the horizontal highest fold axis
σ[SUB]h [/SUB]or [SUB]d[/SUB] (horizontal)	reflection of the molecule horizontally compared to the horizontal highest fold axis
i	Inversion of the molecule from the center
S[SUB]n[/SUB]	rotation of 2π/n and then reflected in a plane perpendicular to rotation axis
#C[SUB]n[/SUB]	the # stands for the number of irreducible representation for the C[SUB]n[/SUB]
#σ	the # stands for the number irreducible representations for the sigmas
the number in superscript	in the same rotation there is another rotation, for instance O[SUB]h[/SUB] has 3C[SUB]2[/SUB]=C[SUB]4[/SUB][SUP]2[/SUP]
other useful definitions
(R[SUB]x[/SUB],R[SUB]y[/SUB])	the ( , ) means they are the same and can be counted once
x[SUP]2[/SUP]+y[SUP]2[/SUP], z[SUP]2[/SUP]	without ( , ) means they are different and can be counted twice

Looking at a Character Table

​

D[SUB]3[/SUB]h​	E​	2C[SUB]3[/SUB]​	3C[SUB]2[/SUB]​	σ[SUB]h[/SUB]​	2S[SUB]3[/SUB]​	3σ[SUB]v[/SUB]​	IR​	Raman​
A[SUB]1[/SUB]'​	1​	1​	1​	1​	1​	1​	​	x[SUP]2[/SUP]+y[SUP]2[/SUP], z[SUP]2[/SUP]​
A[SUB]2[/SUB]'​	1​	1​	-1​	1​	1​	-1​	R[SUB]z[/SUB]​	​
E'​	2​	-1​	0​	2​	-1​	0​	(x,y)​	x[SUP]2[/SUP]-y[SUP]2[/SUP], xy ​
A[SUB]1[/SUB]"​	1​	1​	1​	-1​	-1​	-1​	​	​
A[SUB]2"[/SUB]​	1​	1​	-1​	-1​	-1​	1​	z​	​
E"​	2​	-1​	0​	-2​	1​	0​	(R[SUB]x[/SUB], R[SUB]y[/SUB])​	(xy, yz)​

The order is the number in front of the the classes. If there is not number then it is considered to be one. The number of classes is the representation of symmetries.The D[SUB]3[/SUB]h has six classes and an order of twelve

​

understanding using matrix

The identity does nothing to the matrix
[1 0 0] [X] [X]
[0 1 0] [Y] = [Y]
[1 0 1] [Z] [Z]
σ[SUB]([/SUB][SUB]xy)[/SUB] the x and y stay positive, while z turns into a negative.
[1 0 0] [X] [X]
[0 1 0] [Y] = [Y]
[1 0 -1] [Z] [-Z]

Inverion (I) is when all of the matrix turns into a negative
[-1 0 0] [X] [-X]
[0 -1 0] [Y] = [-Y]
[1 0 -1] [Z] [-Z]
C[SUB]n [/SUB]is when one would use cos and sin. for an example C[SUB]4[/SUB]
[cos (2π/4 -sin (2π/4 0] [X] []
[sin (2π/4) cos (2π/4) 0] [Y] = []
[0 0 1] [Z] []







Character Table

A character table is a table whose rows correspond to irreducible group representation, and whose columns correspond to classes of group elements. It is used to used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons

Every point group has a character table associated with it

C[SUB]2v[/SUB]	E	C[SUB]2[/SUB]	(σ[SUB]v[/SUB] (xz	(σ[SUB]v [/SUB](yz
A[SUB]1[/SUB]	1	1	1	1	z	x[SUP]2[/SUP], y[SUP]2[/SUP], z[SUP]2[/SUP]
A[SUB]2[/SUB]	1	1	-1	-1	R[SUB]z[/SUB]	xy
B[SUB]1[/SUB]	1	-1	1	-1	x, R[SUB]y[/SUB]	xz
B[SUB]2[/SUB]	1	-1	-1	1	y, R[SUB]x[/SUB]	yz

The point group is located at the top left-hand corner of the table. The symmetry operations are indicated across the top row of the character table

The symmetry lables are indicated on the first column, after the point group. Symmetry labels tell about degeneracies. A and B mean single, non-degenerate. E means doubly degenerate. T refers to triply degenerate



For example, H[SUB]2[/SUB]O belongs to C[SUB]2[/SUB]v point group. For this molecule, reading from the character table, the symmetry elements are E, C[SUB]2, [/SUB]σ[SUB]v[/SUB](xz), and σ[SUB]v[/SUB](yz). The symmetry labels for H[SUB]2[/SUB]O is A[SUB]1[/SUB], A[SUB]2[/SUB], B[SUB]1[/SUB], and B[SUB]2[/SUB]


The last two columns in the character table describes whether a symmetry is IR or Raman active, or both IR and Raman active. For example, for water, the rotational vibration modes are 2A[SUB]1[/SUB] and B[SUB]1[/SUB]. Based on the character table of C[SUB]2v[/SUB], A[SUB]1[/SUB] transforms z, x[SUP]2[/SUP], y[SUP]2[/SUP], and z[SUP]2. [/SUP]Hence, A[SUB]1[/SUB] is both IR and Raman active. B[SUB]1[/SUB] transforms and xz, so B[SUB]1 [/SUB]is Raman active

IR active	Raman active
x,y,z	x[SUP]2[/SUP], y[SUP]2[/SUP], z[SUP]2[/SUP]
	xy, yz, xz

Common point group and their symmetry elements


C1: E

Cs: E, sh

Ci: E, i

Cn: E, Cn

Dn (n = odd): E, Cn, n^C2

Dn (n = even E): Cn, n/2^C2´, n/2^C2´´

Cnv (n = odd): E, Cn, nsv

Cnv (n = even): E, Cn, n/2sv, n/2sd

Cnh (n = odd): E, Cn, sh, Sn

Cnh (n = even): E, Cn, sh, Sn, i

Dnh (n = odd): E, Cn, sh, n^C2, Sn, nsv

Dnh (n = even): E, Cn, sh, n/2^C2´, n/2^C2´´, Sn, n/2sv, n/2sd, i

Dnd (n = odd): E, Cn, n^C2, i, S2n, nsd

Dnd (n = even): E, Cn, nC2´, S2n, nsd

Sn (n = even): only E, Sn, Cn/2 and i if n/2 odd

T: E, 4C3, 3C2

Th: E, 4C3, 3C2, 4S2n, i, 3sh

Td: E, 4C3, 3C2, 3S4, 6sd

O: E, 3C4, 4C3, 6C2

Oh: E, 3C4, 4C3, 6C2, 4S6, 3S4, i, 3sh, 6sdI E, 6C5, 10C3, 15C2

Ih: E, 6C5, 10C3, 15C2, i, 6S10, 10S6, 15s

Kh: E, infinite numbers of all symmetry elements






BF[SUB]3
[/SUB]
D[SUB]3h[/SUB]

E, 2C[SUB]3[/SUB], 3C[SUB]2[/SUB], σ[SUB]h[/SUB], 2S[SUB]3[/SUB], and 3σ[SUB]v[/SUB]

modes are observed: A[SUB]1[/SUB]', 2E', and A[SUB]2[/SUB]

A[SUB]1[/SUB]' : Raman active; E' : IR + Raman active; A[SUB]2[/SUB]" : IR active

Two bands are observed for IR spectrum and two bands are observe for Raman spectrum

​

 

[S H i M A]

نظریه گروه در شیمی:

Group Theory and its Application to Chemistry



Group Theory is the mathematical application of symmetry to an object to obtain knowledge of its physical properties. What group theory brings to the table, is how the symmetry of a molecule is related to its physical properties and provides a quick simple method to determine the relevant physical information of the molecule. The symmetry of a molecule provides you with the information of what energy levels the orbitals will be, what the orbitals symmetries are, what transitions can occur between energy levels, even bond order to name a few can be found, all without rigorous calculations. The fact that so many important physical aspects can be derived from symmetry is a very profound statement and this is what makes group theory so powerful

To a fully understand the math behind group theory one needs to take a look at the theory portion of the Group Theory topic or refer to one of the reference text listed at the bottom of the page. Never the less as Chemist the object in question we are examining is usually a molecule. Though we live in the 21[SUP]st[/SUP] century and much is known about the physical aspects that give rise to molecular and atomic properties. The number of high level calculations that need to be performed can be both time consuming and tedious. To most experimentalist this task is takes away time and is usually not the integral part of their work. When one thinks of group theory applications one doesn't necessarily associated it with everyday life or a simple toy like a Rubik's cube. A Rubik's cube is an a cube that has a 3X3 array of different colored tiles on each of its six surfaces, for a total of 54 tiles. Since the cube exist in 3D space, the three axis are x,y,z. Since the rubik's cube only allows rotation which are called operations, there are three such operations around each of the x,y,z axis

Of course the ultimate challenge of a Rubik's cube is to place all six colors on each of the six faces. By performing a series of such operations on the Rubik's cube one can arrive at a solution (A link of a person solving a Rubik's cube[SUP]1[/SUP] in 10.4s with operations performed noted, the operations performed will not translate to chemistry applications but it is a good example of how symmetry operations arrive at a solution).The operations shown in the Rubik's cube case are inherent to the make up of the cube, ie the only operations allowed are the rotations along the x,y,z axis. Therefore the Rubik's cube only has x,y,z rotation operations. Similarly the operations that are specific to a molecule are dependent on its symmetry. These operations are given in the top row of the character table

The character table contains a wealth of information, for a more detailed discussion of the character table can be found in Group Theory Theoretical portion of the chem-wiki. All operations in the character table are contained in the first row of the character table, in this case E, C[SUB]3[/SUB], & ?v, these are all of the operations that can be preformed on the molecule that return the original structure. The first column contains the three irreducible representations from now on denoted as ?ir, here they are A1, A2 & E. The value of the ?ir denotes what the operation does. A value of 1 represents no change, -1 opposite change and 0 is a combination of 1 & -1 (0’s are found in degenerate molecules. The final two columns Rotation and Translation represented by R[SUB]x[/SUB],R[SUB]y[/SUB],R[SUB]z[/SUB] & x,y,z respectively. Where R's refer to rotation about an axis and the x,y,z refers to a translation about an axis, the ?ir the each R[SUB]x,[/SUB] R[SUB]y[/SUB], R[SUB]z[/SUB] & x,y,z term is the irreducible symmetry of a rotation or translation operation. Like wise the final column the orbital symmetries relates the orbital wavefunction to a irreducible representation



Direct Products


This is a quick rule to;follow for calculating the direct product, such a calculation will be necessary for working through the transition moment integral. Following the basic rules given by the table given below. One can easily work through symmetry calculations very quickly

Vibrations


All molecules vibrate. While these vibrations can originate from several events, which will be covered later, the most basic of these occurs when an electron is excited within the electronic state from one eigenstate to another. The Morse potential (electronic state) describes the energy of the eigenstate as a function of the interatomic distance. When an electron is excited form one eigenstate to another within the electronic state there is a change in interatomic distance, this result in a vibration occurring

Vibrational energies arise from the absorption of polarizing radiation. Each vibrational state is assigned a ?ir. A vibration occurs when an electron remains within the electronic state but changes from one eigenstate to another (The vibrations for the moment are only IR active vibrations, there are also Raman vibrations which will be discussed later in electronic spectroscopy), in the case of the Morse diagram above the eigenstates are denoted as v. As you can see from the diagram the eigenstate is a function of energy versus interatomic distance

To predicting whether or not a vibrational transition, or for that matter a transition of any kind, will occur we use the transition moment integral

The transition moment integral is written here in standard integral format, but this is equivalent to Bra & Ket format which is standard in most chemistry quantum mechanical text (The ?i is the Bra portion, ?f is the Ket portion). The transition moment operator ? is the operator the couples the initial state ?i to the final state ?f , which is derived from the time independent Schrödinger equation.3 However using group theory we can ignore the detailed mathematical methods. We can use the ?ir of the vibrational energy levels and the symmetry of the transition moment operator to find out if the transition is allowed by selection rules. The selection rules for vibrations or any transition is that is allowed, for it to by allowed by group theory the answer must contain the totally symmetric ?ir, which is always the first ?ir in the character table for the molecule in question





Symmetry

Let’s work through an example: Ammonia NH3. The ammonia molecule below has C3v symmetry associated with it. Meaning all of the properties contained in the C3v character table above are pertinent to the ammonia molecule

The principle axis is the axis that the highest order rotation can be preformed. In this case the z-axis pass through the lone pairs (pink sphere), which contains a C3 axis. The ?’s or mirror planes (?v parallel to z-axis & ?h perpendicular to the z-axis). In ammonia there is no ?h only three ?v’s. The combination of C3 & ?v leads to C3v point group, which leads to the C3v character table.

The number of transitions is dictated by 3N-6 for non-linear molecules and 3N-5 for linear molecules, where N is the number of atoms. The 6 & the 5 derive from three translations in the x,y,z plan and three rotations also in the x,y,z plan. Where a linear molecule only has two rotations in the x & y plans since the z axis has infinite rotation. This leads to only 5 degrees of freedom in the rotation and translation operations. In the case of Ammonia there will be 3(4)-6=6 vibrational transitions. This can be confirmed by working through the vibrations of the molecule. This work is shown in the table below

The vibrations that are yielded 2A1 & 2E (where E is doubly degenerate, meaing two vibration modes each) which total 6 vibrations. This calculation was done by using the character table to find out the rotation and translation values and what atoms move during each operation. Using the character table we can characterize the A1 vibration as IR active along the z-axis and raman active as well. The E vibration is IR active along both the x & y axis and is Raman active as well. From the character table the IR symmetries correspond to the x, y & z translations. Where the Raman active vibrations correspond to the symmetries of the d-orbitals




Vibrational Spectroscopy



Infrared pectroscopy


Infrared Spectroscopy (IR) measures the vibrations that occur within a single electronic state, such as the one shown above. Because the transition occurs within a single electronic state there is a variation in interatomic distance. The dipole moment is dictate by the equation

Where ? magnitude of dipole moment; ? is the polarizability constant & ? is the magnitude of the electric field which can be described as the electronegitivity.3 Therefore when a vibration occurs within a single electronic state there is a change in the dipole moment, which is the definition of an active IR transition

In terms of group theory a change in the dipole is a change from one vibrational state to another, as shwon by the equation above. A picture of the vibrational states with respect ot the rotational states and electronic states is given below. In IR spectroscopy the transition occurs only from on vibrational state to another all within the same electronic state, shown below as B

Electronic Transitions


When an electron is excited from one electronic state to another, this is what is called an electronic transition. A clear example of this is part C in the energy level diagram shown above. Just as in a vibrational transition the selection rules for electronic transitions are dictated by the transition moment integral. However we now must consider both the electronic state symmetries and the vibration state symmetries since the electron will still be coupled between two vibrational states that are between two electronic states. This gives us this modified transition moment integral

Where you can see that the symmetry of the initial electronic state & vibrational state are in the Bra and the final electronic and vibrational states are in the Ket. Though this appears to be a modified version of the transition moment integral, the same equation holds true for a vibrational transition. The only difference would be the electronic state would be the same in both the initial and final states. Which the dot product of yields the totally symmetric representation, making the electronic state irrelevant for purely vibrational spectroscopy


Raman


In resonate Raman spectroscopy transition that occurs is the excitation from one electronic state to another and the selection rules are dictated by the transition moment integral discussed in the electronic spectroscopy segment. However mechanically Raman does produce a vibration like IR but the selection rules for Raman state there must be a change in the polarization, that is the volume occupied by the molecule must change. But as far as group theory to determine whether or not a transition is allowed one can use the transition moment integral presented in the electronic transition portion. Where one enters the starting electronic state symmetry and vibrational symmetry and final electronic state symmetry and vibrational state, perform the direct product with the different M's or polarizing operators For more information about this topic please explore the Raman spectroscopy portion of the Chemwiki




Fluorescence


For the purposes of Group Theory Raman and Fluorescence are indistinguishable. They can be treated as the same process and in reality they are quantum mechanically but differ only in how Raman photons scatter versus those of fluorescence


Phosphorescence


Phosphorescence is the same as fluorescence except upon excitation to a singlet state there is an interconversion step that converts the initial singlet state to a triplet state upon relaxation. This process is longer than fluorescence and can last microseconds to several minutes. However despite the singlet to triplet conversion the transition moment integral still holds true and the symmetry of ground state and final state still need to contain the totally symmetric representation




Molecular Orbital Theory and Symmetry


Molecular Orbitals also follow the symmetry rules and indeed have their own ?ir. Below are the pi molecular orbitals for trans-2-butene and the corresponding symmetry of each molecular orbital

The ? ir of the molecular orbitals are created by simply preforming the operations of that molecule's character table on that orbital. In the case of trans-2-butene the point group is C2h, the operations are: E, C2, i & ?h. Each operation will result in a change in phase (since were dealing with p-orbitals) or it will result in no change. The first molecular orbital results in the totally symmetric representation, working through all four operations E, C2, i, ?h will only result in 1's meaning there is no change, giving the Ag symmetry state. These molecular orbitals also represent different electronic states and can be arranged energetically. Putting the orbital that has the lowest energy, the orbital with the fewest nodes at the bottom of the energy diagram and like wise working up form lowest energy to highest energy. The highest energy orbital will have the most nodes. Once you've set up your MO diagram and place the four pi electrons in the orbitals you see that the first two orbitals listed (lowest energy) are HOMO orbitals and the bottom two (highest energy) and LUMO orbitals. With this information if you have a transition from the totally symmetric HOMO orbital to the totally symmetric LUMO orbital the transition moment operator would need to have Ag symmetry (using the C2h) to give a result containing the totally symmetric representation

These four molecular orbitals represent four different electronic states. So transitions from one MO into another would be something that is measured typically with UV-Vis spectrometer




​

 

[S H i M A]

​

تئوری نظریه گروه در شیمی:

Group Theory: Theory
​

Symmetry can help resolve many chemistry problems and usually the first step is to determine the symmetry. If we know how to determine the symmetry of small molecules, we can determine symmetry of other targets which we are interested in. Therefore, this module will introduce basic concepts of group theory and after reading this module, you will know how to determine the symmetries of small molecules


Introduction
​

Symmetry is very important in chemistry researches and group theory is the tool that is used to determine symmetry. Usually, it is not only the symmetry of molecule but also the symmetries of some local atoms, molecular orbitals, rotations and vibrations of bonds, etc. that are important. For example, if the symmetries of molecular orbital wave functions are known, we can find out information about the binding. Also, by the selection rules that are associated with symmetries, we can explain whether the transition is forbidden or not and also we can predict and interpret the bands we can observe in Infrared or Raman spectrum.
Symmetry operations and symmetry elements are two basic and important concepts in group theory. When we perform an operation to a molecule, if we cannot tell any difference before and after we do the operation, we call this operation a symmetry operation. This means that the molecule seems unchanged before and after a symmetry operation. As Cotton defines it in his book, when we do a symmetry operation to a molecule, every points of the molecule will be in an equivalent position



Chemical Applications of Group Theory

Symmetry Elements
​

For different molecules, there are different kinds of symmetry operations we can perform. To finish a symmetry operation, we may rotate a molecule on a line as an axis, reflect it on a mirror plane, or invert it through a point located in the center. These lines, planes, or points are called symmetry elements. There may be more then one symmetry operations associated with a particular symmetry




Identity E​

The molecule does not move and all atoms of the molecule stay at the same place when we apply an identity operation, E, on it. All molecules have the identity operation. Identity operation can also be a combination of different operations when the molecule returns to its original position after these operations are performed.[SUP]1[/SUP] This will be demonstrated later



Proper Rotations and Cn axis
​

C[SUB]n[/SUB] generates n operations, whose symbols are C[SUB]n[/SUB], C[SUB]n[/SUB][SUP]2[/SUP], C[SUB]n[/SUB][SUP]3[/SUP], C[SUB]n[/SUB][SUP]4[/SUP],…, E =C[SUB]n[/SUB][SUP]n[/SUP]However, we usually write them in another way. Table 1.2 shows the way we write the 6 operations generated by proper rotation C[SUB]6[/SUB]. From this table, we can see that the symbols of the 6 rotations generated by C[SUB]6[/SUB] are C[SUB]6[/SUB], C[SUB]3[/SUB], C[SUB]2[/SUB], C[SUB]3[/SUB][SUP]2[/SUP], C[SUB]6[/SUB][SUP]5[/SUP], E.One molecule can have many proper axes and the one with the largest n is called principle axis

Table 1.2 C[SUB]6[/SUB] axis and operations it generates

Reflection and mirror plane σ
​

Take NH[SUB]3[/SUB] for an example. There are 3 mirror planes in molecule NH[SUB]3[/SUB]. When we do a reflection through a mirror plane, molecule NH[SUB]3 [/SUB]dose not change - Figure 1.2

Figure 1.2 A mirror plane of NH[SUB]3[/SUB].



There are three different kinds of mirror plane, ?[SUB]v[/SUB], ?[SUB]h[/SUB], and ?[SUB]d[/SUB]. The mirror plane that contains the principle axis is called ?[SUB]v[/SUB]<-[if><xml> <oleobject type="Embed" progid="Equation.DSMT4" shapeid="_x0000_i1025" drawaspect="Content" objectid="_1296914671"> </oleobject> </xml>.The mirror plane that perpendicular to the principle axis is called σ[SUB]h[/SUB].[SUP]2[/SUP]Figure 1.3 shows σ[SUB]v[/SUB], σ[SUB]h[/SUB], and σ[SUB]d[/SUB] in PtCl[SUB]4[/SUB][SUP]2

[/SUP]

Figure 1.3 ?[SUB]v[/SUB], ?[SUB]h[/SUB], and ?[SUB]d[/SUB] of PtCl[SUB]4[/SUB][SUP]2-[/SUP].This picture is drawn by ACD Labs 11.0

When mirror plane is operated n times, we have[SUP]1

[/SUP]

Inversion and inversion center i
​

In a molecule, if we can find a point, on the straight line through which we can find a pair of same atoms on both side of this point, we call this molecule has an inversion center. The inversion center, i, is not necessarily on an atom of the molecule.[SUP]1[/SUP]Figure 1.4 shows the inversion center of C[SUB]2[/SUB]H[SUB]4[/SUB]Cl[SUB]2[/SUB].When inversion is operated n times, we have[SUP]1

[/SUP]

[SUP]

[/SUP]
Figure 1.4 Inversion center of C[SUB]2[/SUB]H[SUB]4[/SUB]Cl[SUB]2


[/SUB]



Improper Rotations and S[SUB]n[/SUB] axis
​

Improper rotation is a combination of two operations, proper rotation C[SUB]n[/SUB] and reflection ?. Figure 1.5 shows the improper rotation operation in CH[SUB]4[/SUB].
Table 1.3 and table 1.4 show the operations generated by S[SUB]6[/SUB] and S[SUB]5[/SUB] axes separately. The 6 operations generated by S[SUB]6[/SUB] axis are S[SUB]6[/SUB], C[SUB]3[/SUB], i, C[SUB]3[/SUB][SUP]2[/SUP], S[SUB]6[/SUB][SUP]5[/SUP] and E. And the 10 operations generated by S[SUB]5[/SUB]axis are S[SUB]5[/SUB], C[SUB]5[/SUB][SUP]2[/SUP], S[SUB]5[/SUB][SUP]3[/SUP], C[SUB]5[/SUB][SUP]4[/SUP], ?, C[SUB]5[/SUB], S[SUB]5[/SUB][SUP]7[/SUP], C[SUB]5[/SUB][SUP]3[/SUP], S[SUB]5[/SUB][SUP]9[/SUP] and E.[SUP]1[/SUP]Since S[SUB]1[/SUB]= ?[SUB]h[/SUB] and S[SUB]2[/SUB]=σ[SUB]h[/SUB]C[SUB]2[/SUB]=i, the order of improper rotation, n, must always be larger than 2. And generally, when n is even, there are n operations {S[SUB]n[/SUB][SUP]1[/SUP], S[SUB]n[/SUB][SUP]2[/SUP], ..., S[SUB]n[/SUB][SUP]n[/SUP]}, while when n is odd, there are 2n operations {S[SUB]n[/SUB][SUP]1[/SUP], S[SUB]n[/SUB][SUP]2[/SUP], ..., S[SUB]n[/SUB][SUP]2n[/SUP]}. And we have[SUP]1

[/SUP]

Table 1.3
S[SUB]6[/SUB] axis and operations it generates

Table 1.4 S[SUB]5[/SUB] axis and operations it generates

Figure 1.5 Improper rotation operation S[SUB]4[/SUB] in CH[SUB]4

[/SUB]

[SUB]

[/SUB]
​

Symmetry Point Groups​

Definition and Properties of a Group
​

For a molecule, all the symmetry operations that can be applied to the molecule have all the properties of a group. Therefore, before we introduce the symmetry point groups, the concept and properties of a group will be introduced first. When some elements have a certain kind of relationships and can be related to each other by these relationships, these elements can form a group



Closure
​

If two elements A and B are in the group G, then the multiplicity of these two elements, C, is also in this group. It can be expressed as

Associativity
​

All the elements in the group must satisfy the law of associativity, which can be expressed as
(AB)C=A(BC)

Identity
​

The group must contain such an element E that
ER=RE=R
In group theory, it refers to the operation identity E. Because any molecule or substance must at least have the symmetry element E


Inverses


If A is an element in group G, there must be another element A[SUP]-1[/SUP] in group G that satisfies AA[SUP]-1[/SUP]= A[SUP]-1[/SUP]A=E. Usually we can write A[SUP]-1[/SUP] as B. It can be expressed as
If A?G and AA[SUP]-1[/SUP]= A[SUP]-1[/SUP]A=E then A[SUP]-1[/SUP]=B=G

​

 

[S H i M A]

Group Multiplication Tables
​

If there are n elements in a group G, and all of the possible n[SUP]2[/SUP] multiplications of these elements are known, then this group G is unique and we can write all these n[SUP]2[/SUP] multiplications in a table called group multiplication table. All the symmetry operations of a molecule can be written in the form of group multiplication table. There is a very important rule about group multiplication tables called rearrangement theorem, which is that every element will only appear once in each row or column.[SUP]1[/SUP]In group theory, when the column element is A and row element is B, then the corresponding multiplication is AB, which means B operation is performed first, and then operation A follows.[SUP]1 [/SUP]
Table 2.1 Group multiplication table[SUP]1

[/SUP]​

G[SUB]6[/SUB]	E	A	B	C	D	F
E	E	A	B	C	D	F
A	A	E	D	F	B	C
B	B	F	E	D	C	A
C	C	D	F	E	A	B
D	D	C	A	B	F	E
F	F	B	C	A	E	D

Subgroups
​

From table 2.1 above, we can find several small groups in the group multiplication table. For example

​

G[SUB]2[/SUB]	E	A
E	E	A
A	A	E

In the same way, there are also many several small groups with orders 1, 2, 3 respectively. These small order groups that can be found in a higher order group are called subgroups. The number of elements in a group is called the order of a group, using a symbol h. The number of elements consist a subgroup is called the order of a subgroup, using a symbol g. From the previous two examples, we have[SUP]1[/SUP]

(h/g=k (k is a whole number

Since the symmetry point group have all the properties of a group, there are also several subgroups that we can find in a perticular symmetry point group. And sometimes we just use symmetry opertaions in one subgroup to apply to a system instead of using all the symmetry operations in the group, which can significantly simplify the calculations




Classes
​

Class is another important concept in group theory which provides a way to simplify the expression of all the symmetry operations in a group. This means that we do not have to write down all the symmetry operatoins in a group but combine some related operations instead. The followin part will introduce the concept of classes and how to divide a group into classes



Similarity transformation and conjugate
​

A and B are two elements in a group, X is any elements in this group. If
X[SUP]-1[/SUP]AX=B
Then we can say the relationship of A and B is similarity transformation. A and B are conjugate. [SUP]1

[/SUP]
Conjugate elements have three properties[SUP]1

[/SUP]
a) Every element is conjugate with itself

A=X[SUP]-1[/SUP]AX


b) If A is conjugate with B, then B is conjugate with A
If A=X[SUP]-1[/SUP]BX, then B=Y[SUP]-1[/SUP]AY


c) If A is conjugate with B and C, then B is conjugate with C
If A=X[SUP]-1[/SUP]BX and A=Y[SUP]-1[/SUP]CY, then B=Z[SUP]-1[/SUP]CZ


Classes
​

Now we can define a class. A class of a group is defined as all the elements in the group that are conjugated to each other.[SUP]1[/SUP]


How to determine the classes of a group
​

To determine the classes of a group, we need to apply similarity transformation to the elements in the group until all the elements are grouped into smaller sets. For example, there are four elements in a group

{E, C[SUB]2[/SUB], σ[SUB]v[/SUB], σ[SUB]v[/SUB][SUP]’[/SUP]}

X= E, C[SUB]2[/SUB], ?[SUB]v[/SUB], ?[SUB]v[/SUB][SUP]’ [/SUP]X[SUP]-1[/SUP]= E, C[SUB]2[/SUB], σ[SUB]v[/SUB], σ[SUB]v
[/SUB]
Because we always have XEX[SUP]-1[/SUP]=E, {E} is always a class for any point group. Then, apply similarity transformation to other elements in the group until all the elements are classified in smaller sets. Table 2.3 shows how the elements are classified in to classes


Table 2.4 Classes six order group

Therefore, there are three classes in group C[SUB]3v[/SUB]: {E}, {C[SUB]3[/SUB], C[SUB]3[/SUB][SUP]2[/SUP]} and { σ[SUB]v[/SUB], σ[SUB]v[/SUB] [SUP]‘[/SUP], σ[SUB]v[/SUB] '‘ }


Significance of classes of a group

In the same class of a group, the operations can be converted to each other by an operation. The operations in the same class are called equivalent operations. And a class of a symmetry group is a group of equivalent operations. This gives a simpler way to express the operations in a group.[SUP]1[/SUP]For example, for operations in the six order group above, table 2.5 shows the new way to express these operations


Table 2.5 Ways to express operations in six order group

Symmetry Point Groups​

As what mantioned above, all the symmetry operations of a molecule as a group can be written in the form of group multification table and they obey all the properties of a group. This group is called symmetry point group. It is called point group for two reasions. First reason is that this group have all the properties of a group in mathmeths. Second reason is that all the symmetry operations are related to a fixed point in the molecue, which is not necessearily to be an atom of the molecule. According to the symmetry of molecules, they can be classified as symmetry point groups.[SUP]1[/SUP]

To determine the symmetry point group of a molecule is very important, because all symmetry related properties are dependent on the symmetry point group of the molecule. Symmetry point groups can be divided into 5 classes which are summaried below and the they are described in details here (symmetry point groups).[SUP]1,6
[/SUP]​

​

​	Point groups ​	Symmetry Elements ​	Order ​	Example ​
Nonaxial​	C[SUB]1 [/SUB]​	E ​	1 ​	HCFBrCl ​
​	C[SUB]i[/SUB]​	E, i​	2​	C[SUB]2[/SUB]H[SUB]2[/SUB]F[SUB]2[/SUB]Cl[SUB]2 [/SUB] ​
​	C[SUB]s[/SUB]​	E, ?​	2​	CH[SUB]2[/SUB]BrCl ​
Cyclic​	C[SUB]n[/SUB]​	E, C[SUB]n[/SUB]​	n​	C[SUB]2[/SUB]H[SUB]4[/SUB]Cl[SUB]2[/SUB] ​
​	C[SUB]nh[/SUB]​	E, C[SUB]n[/SUB], n?[SUB]v[/SUB]​	2n​	NH[SUB]3 [/SUB] ​
​	C[SUB]nv[/SUB]​	E, C[SUB]n[/SUB], σ[SUB]h[/SUB], S[SUB]n[/SUB]​	2n​	C[SUB]2[/SUB]H[SUB]2[/SUB]F[SUB]2 [/SUB] ​
​	S[SUB]n[/SUB]​	E, S[SUB]n[/SUB]​	n​	1,3,5,7 -tetrafluoracyclooctatetrane ​
Dihedral​	D[SUB]n[/SUB]​	E, C[SUB]n[/SUB], nC[SUB]2[/SUB] ([FONT=??]?[/FONT]C[SUB]n[/SUB])​	2n​	[Co(en)[SUB]3[/SUB]][SUP]3+[/SUP]. ​
​	D[SUB]nh[/SUB]​	E, C[SUB]n[/SUB], σ[SUB]h[/SUB], nC[SUB]2[/SUB] ([FONT=??]?[/FONT]C[SUB]n[/SUB])​	4n​	Benzene ​
​	D[SUB]nd[/SUB]​	E, C[SUB]n[/SUB], σ[SUB]d[/SUB], nC[SUB]2[/SUB] ([FONT=??]?[/FONT]C[SUB]n[/SUB])​	4n​	C[SUB]2[/SUB]H[SUB]6[/SUB] ​ ​
Polyhedral​	T[SUB]d[/SUB]​	E, 3C[SUB]2[/SUB], 4C[SUB]3[/SUB], 3S[SUB]4, [/SUB]6σ[SUB]d[/SUB]​	24​	CCl[SUB]4[/SUB] ​
​	O[SUB]h[/SUB]​	E, 3S[SUB]4[/SUB], 3C[SUB]4[/SUB], 6C[SUB]2[/SUB], 4S[SUB]6[/SUB], 4C[SUB]3[/SUB], 3σ[SUB]h[/SUB], 6σ[SUB]d[/SUB], i​	48​	SF[SUB]6[/SUB] ​
​	I[SUB]h[/SUB]​	E, 6S[SUB]10[/SUB], 10S[SUB]6[/SUB], 6C[SUB]5[/SUB], 10C[SUB]3[/SUB], 15C[SUB]2[/SUB], 15?​	120​	C[SUB]60[/SUB] ​
Linear​	C[SUB]?v[/SUB]​	E, C[SUB]?[/SUB], ?σ[SUB]v[/SUB]​	?​	HCl ​
​	D[SUB]?h[/SUB]​	E, C[SUB]?[/SUB] ?σ[SUB]v[/SUB] , σ[SUB]h[/SUB], i, ?C[SUB]2[/SUB]​	? ​	O[SUB]2[/SUB] ​

​

 

[S H i M A]

Determination of symmetry Point Groups
​

Determination of symmetry point group of a molecule is the very first step when we are solving chemistry problems. The symmetry point group of a molecule can be determined by the following flow chart


Table 2.12 Flow chart to determine point group

Now, using this flow chart, we can determine the symmetry of molecules. However, to further determine the symmetry properties of something such as molecular orbitals, vibrational modes, etc. we need character tables which will be introduced next



Character Tables
​

Representations of a Group
​

Through similarity of transformation, we can define the reducible and irreducible representations of a group. If a matrix representation A can be transferred to block-factored matrix A’, a matrix composed of blocks (A’, A’’, A’’’) at the diagonal and zero in any other position, by similarity transformation, this matrix A is called the reducible representation of this group. And if these blocks (A’, A’’, A’’’) cannot be further transferred to block-factored matrix through similarity transformation, A’, A’’, A’’’ are called irreducible representations of the group. And the sum of the trace of A’, A’’, A’’’ (the number on the diagonal of A’, A’’, A’’’) is called the characters of this representation. As is shown in the following equation, a[SUB]11[/SUB]’+ a[SUB]22[/SUB]’+…+ a[SUB]nn[/SUB]’ is one of the characters. Reducible representations can be reduced to irreducible representations and irreducible representations cannot be reduced further

Take C[SUB]3v[/SUB] as an example.Take (x, y, z) as the basic, the matrix of all the operations in C[SUB]3v[/SUB] group {E, C[SUB]3[/SUB], C[SUB]3[/SUB][SUP]2[/SUP], σ[SUB]v[/SUB], σ[SUB]v[/SUB] [SUP]‘[/SUP], σ[SUB]v[/SUB] [SUP]'‘[/SUP]} are shown in Table 2.6



Table 2.6 Reducible and irreducible representations of C[SUB]3v

[/SUB]

As shown in the table 2.6, all the matrix are block-factored matrix and they are reducible representations. Every block in these reducible representations are irreducible representations and the sums of the trace are the characters which are also listed in the table. Notice that the operations in the same class have the same character. Therefore, they are always written together using the new notations {E, 2C[SUB]3[/SUB], 3σ[SUB]v[/SUB]



Table 2.7 Two irreducible representations of C[SUB]3v

[/SUB]

This is not a completed table of irreducible representations, because the basis chosen are not completed. There are different kinds of basis, including one-dimensional basis like x, y, z, R[SUB]x[/SUB], R[SUB]y[/SUB], R[SUB]z[/SUB] and two-dimensional basis like x[SUP][SUB]2[/SUB][/SUP], y[SUP]2[/SUP], z[SUP]2[/SUP], xy, yz, xz. If we chose R[SUB]z[/SUB] which is the rotation around z-axis as another basis, we can get another irreducible representation, (1, 1, -1). “1” means nothing change when operation is applied to the basis. “-1” means it becomes opposite when operation is applied to the basis. “0” means the basis are moved when operation is applied. Therefore, in summary, for now the irreducible representations of C[SUB]3v[/SUB] group is


Table 2.8 Summary of irreducible representations of C[SUB]3v

[/SUB]

​

Five rules of Characters
​

For irreducible representations and their characters, there are five very important rules[SUP]1

[/SUP]

Rule 1
​

The order of the irreducible representation matrix is called the dimension of the irreducible representation, using symbol l[SUB]1[/SUB], l[SUB]2[/SUB], ... And rule 1 states that the sum of the squares of all the dimensions of irreducible representations (l[SUB]1[/SUB][SUP]2[/SUP]+ l[SUB]2[/SUB][SUP]2[/SUP]+ …) is equal to the order of the group, h.
?l[SUB]i[/SUB][SUP]2[/SUP]=l[SUB]1[/SUB][SUP]2[/SUP]+ l[SUB]2[/SUB][SUP]2[/SUP]+ …=h

Since the character of the irreducible representation of operation E, ?[SUB]i[/SUB](E), is equal to the dimension of the corresponding irreducible representation, Rule 1 can also be written as

? Γ[SUB]i[/SUB](E)[SUP]2[/SUP]= Γ[SUB]1[/SUB](E)[SUP]2[/SUP]+ Γ[SUB]2[/SUB](E)[SUP]2[/SUP]+ …=h

Rule 2
​

Rule 2 is that the sum of the square of the characters in any irreducible representation is equal to h. For example, for the first irreducible representation in C[SUB]3v[/SUB] group
Γ[SUB]1[/SUB](E)[SUP]2[/SUP]+ Γ[SUB]1[/SUB](C[SUB]3[/SUB])[SUP]2[/SUP]+ Γ[SUB]1[/SUB](C[SUB]3[/SUB][SUP]2[/SUP])[SUP]2[/SUP]+ Γ[SUB]1[/SUB](σ[SUB]v[/SUB])[SUP]2[/SUP]+ Γ[SUB]1[/SUB](σ[SUB]v[/SUB] [SUP]‘[/SUP])[SUP]2[/SUP]+ Γ[SUB]1[/SUB](σ[SUB]v[/SUB] [SUP]'‘[/SUP])[SUP]2[/SUP]=1[SUP]2[/SUP]+1[SUP]2[/SUP]+1[SUP]2[/SUP]+1[SUP]2[/SUP]+1[SUP]2[/SUP]+1[SUP]2[/SUP]=6
Since for the same class, the characters are the same, it can also be written as
Γ[SUB]1[/SUB](E)[SUP]2[/SUP]+ 2*Γ[SUB]1[/SUB](C[SUB]3[/SUB])[SUP]2[/SUP]+ 3* Γ[SUB]1[/SUB](σ[SUB]v[/SUB])[SUP]2[/SUP]=1[SUP]2[/SUP]+2*1[SUP]2[/SUP]+3*1[SUP]2[/SUP]=6
Also, for another irreducible representation in C[SUB]3v[/SUB] group
Γ[SUB]1[/SUB](E)[SUP]2[/SUP]+ 2*Γ[SUB]1[/SUB](C[SUB]3[/SUB])[SUP]2[/SUP]+ 3* Γ[SUB]1[/SUB](σ[SUB]v[/SUB])[SUP]2[/SUP]=2[SUP]2[/SUP]+2*(-1)[SUP]2[/SUP]+3*0[SUP]2[/SUP]=6

Rule 3
​

Rule 3 is that the vectors which composed of the characters from different irreducible representations are orthogonal.
? ?[SUB]i[/SUB](R)[SUP]2[/SUP]Γ[SUB]j[/SUB](R)[SUP]2[/SUP] =0 (i is not equal to j)
Again, take C[SUB]3v[/SUB] group for an example
? Γ[SUB]1[/SUB](R)[SUP]2[/SUP]Γ[SUB]2[/SUB](R)[SUP]2[/SUP] =1*2+2*1*(-1)+3*1*0=0

Rule 4
​

Rule 4 is that the characters of matrix representations, either reducible or irreducible, of the operations in the same class are the same, which is shown as the former table


Rule 5
​

Rule 5 is that the number of irreducible representations is equal to the number of classes

For C[SUB]3v[/SUB] group, there are three classes and therefore there are also three irreducible representations. Therefore, the three irreducible representations in
Table 2.8 are the complete list of irreducible representations in C[SUB]3v[/SUB] group

There is a very important relationship between reducible representations and irreducible representations, which is that any reducible representation can be written as the linear combination of irreducible representations. The similarity transformations do not change the character of a reducible representation, therefore

where ?(R) is the character of reducible representation of operation R. ?[SUB]j[/SUB](R) is the character of jth irreducible representation. a[SUB]j[/SUB] is the times ?[SUB]j[/SUB](R) will appear in blocks when reducible representation is reduced to irreducible representation by similarity transformation. To determine a[SUB]j[/SUB], the former equation can be written as

According to rule 3, only when i=j, the sum over R is not equal to zero. Then according to rule 1, the equation can be written as

Then rearrange to

Using this equation, we can express reducible representations with irreducible representations, which is very important when we solve chemistry problems

Again, take C[SUB]3v[/SUB] group for an example, the reducible representation shown in table 2.6 can be express as combination of irreducible representations using this relationship. Use irreducible representations in table 2.8
a[SUB]1[/SUB]= 1/6 [1(3)(1)+2(0)(1)+3(1)(1)] = 1
a[SUB]1[/SUB]= 1/6 [1(3)(2)+2(0)(-1)+3(1)(0)] = 1
a[SUB]1[/SUB]= 1/6 [1(3)(1)+2(0)(1)+3(1)(-1)] = 0

Therefore

[SUP]5[/SUP]

Table 2.11 Meanings of different area of character tables

Using this flow chart, you can determine the symmetries of small molecules. And also, by using group theory and character tables, you can determine the symmetries of any thing you are interested in, such as molecular orbitals, vibrational modes, etc. In conclusion, group theory play a very important role in chemistry, which we can see from various applications of group theory in chemistry, like Infrared spectrum, Raman spectrum, electronic spectrum, etc



​

 

[S H i M A]

چگونگی تعیین گروه نقطه ای مولکول

​