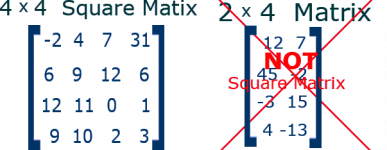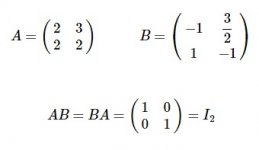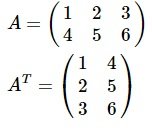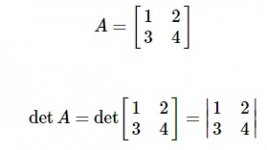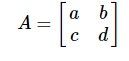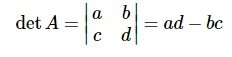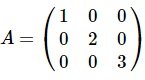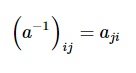فهرست:
- ماتریس مربعی (Square Matrix)
- ماتریس وارون پذیر (Invertible Matrix)(نامنفرد - nonsingular)
- ترانهاده (Transpose) یک ماتریس (Matrix)
- دترمینان (Determinant) یک ماتریس (Matrix)
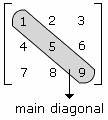
- قطر اصلی (Main diagonal) ماتریس (Matrix)
- ماتریس بالا مثلثی (Upper triangular Matrix)
- ماتریس پایین مثلثی (Lower triangular Matrix)
- ماتریس قطری (Diagonal Matrix)
- ماتریس متعامد (Orthogonal Matrix)