با اجازه دوستان بر این فکر افتادم تا در این تاپیک به اثبات فرمول ها ، حکم ها و قضایای فرمول انجام بدیم ، شاید بعضی از بیان دوستان برای فهم این قضایا ساده تر باشد
اتاق اثبات قضایا ، فرمول ها و حکم های فیزیک
- شروع کننده موضوع آقای سعید حیدری
- تاریخ شروع
قبل از شروع کردن به فرمول ها ابتدا پایه این علمو محکم کنیم :
بدست آوردن و بیان کردن مساحت ها و حجم ها و ...... اجسام
ممنون میشم حجم و مساحت و محیط اشکال هندسی زیر را بهم بگید .
1: مساحت و حجم مکعب
2: مساحت و حجم مکعب مستطیل
3: مساحت و حجم منشور
4: مساحت و حجم استوانه
5: مساحت و حجم هرم
6: مساحت و حجم مخروط
7: مساحت و محیط مثلث
8: مساحت و محیط دایره
اگر بتونین فرمولی بیان کنین که بشه ساده تر اینا رو یاد گرفت
بدست آوردن و بیان کردن مساحت ها و حجم ها و ...... اجسام
ممنون میشم حجم و مساحت و محیط اشکال هندسی زیر را بهم بگید .
1: مساحت و حجم مکعب
2: مساحت و حجم مکعب مستطیل
3: مساحت و حجم منشور
4: مساحت و حجم استوانه
5: مساحت و حجم هرم
6: مساحت و حجم مخروط
7: مساحت و محیط مثلث
8: مساحت و محیط دایره
اگر بتونین فرمولی بیان کنین که بشه ساده تر اینا رو یاد گرفت
| Formula | |
| Rectangle: Area = Length X Width A = lw Perimeter = 2 X Lengths + 2 X Widths P = 2l + 2w |
| Parallelogram Area = Base X Height a = bh |
| Triangle Area = 1/2 of the base X the height a = 1/2 bh Perimeter = a + b + c (add the length of the three sides) |
| Trapezoid Perimeter = area + b1 + b2 + c P = a + b1 + b2 + c |
| Circle.The distance around the circle is a circumference. The distance across the circle is the diameter (d). The radius (r) is the distance from the center to a point on the circle. (Pi = 3.14) More about .circles. d = 2r c = pd = 2 pr A = pr[SUP]2[/SUP] (p=3.14) |
| Rectangular Solid Volume = Length X Width X Height V = lwh Surface = 2lw + 2lh + 2wh |
| Prisms Volume = Base X Height v=bh Surface = 2b + Ph (b is the area of the base P is the perimeter of the base) |
| Cylinder Volume = pr[SUP]2 x [/SUP]height V = pr[SUP]2[/SUP] h Surface = 2p radius x height S = 2prh + 2pr[SUP]2[/SUP] |
| Pyramid V = 1/3 bh b is the area of the base Surface Area: Add the area of the base to the sum of the areas of all of the triangular faces. The areas of the triangular faces will have different formulas for different shaped bases. |
| Cones Volume = 1/3 pr[SUP]2[/SUP] x height V= 1/3 pr[SUP]2[/SUP]h Surface = pr[SUP]2[/SUP] + prs S = pr[SUP]2[/SUP] + prs =pr[SUP]2[/SUP] + pr |
| Sphere Volume = 4/3 pr[SUP]3 [/SUP]V = 4/3 pr[SUP]3 [/SUP]Surface = 4pr[SUP]2 [/SUP]S = 4pr[SUP]2 [/SUP] |
راهنمای استفاده از فرمولها
مساحت A Area
محیط دایره C Circumferenceمساحت A Area
طول L Length
عرض W Width
ارتفاع H Height
شعاع r Radius
1) مساحت مـــربع = یـــک ضلع به توان۲
محیــط مـــربــــع = یک ضلع × 4
2) مساحت مسـتطیـــــــل = طـول × عـرض
محیط مستطیل = ( طول + عرض) × 2
3) مساحت مثلث = ( قاعده × ارتــــــفاع ) تقسیم بر۲ محیط مثلث = مجموع سه ضلع
۴) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع
محیط ذوزنقه = مجموع چهار ضلع
۵) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) تقسیم بر ۲
محیط لوزی = یک ضلع × 4
۶) مساحت متوازی الاضلاع = قاعده × ارتفاع
محیط متوازی الاضلاع = مجموع دو ضلع متوالی × 2
۷) مساحت دایره = عدد پی ( 14/3 ) × شعاع × شعاع
محیط دایره = عدد پی ( 14/3 ) × قطر
۸) مساحت کره = 4 × 14/3 × شعاع به توان دو
حجم کره = چهار سوم × 14/3 × شعاع به توان سه
۹) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3
۱۰ ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش
۱۱ ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع
حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)
۱۲ ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم
۱۳) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحت قاعده × ارتفاع
سطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )
۱۴) مساحت جانبی منشور = مجموع مساحت سطوح جانبی
مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی
۱۵) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
هندسه نااقليدسي و انحناي فضا
هندسه نااقليدسي و انحناي فضا
علومي كه از يونان باستان توسط انديشمندان اسلامي محافظت و تكميل شد، از قرون يازدهم ميلادي به بعد به اروپا منتقل شد، بيشتر شامل رياضي و فلسفه ي طبيعي بود. فلسفه ي طبيعي توسط كوپرنيك، برونو، كپلر و گاليله به چالش كشيده شد و از آن ميان فيزيك نيوتني بيرون آمد. چون كليسا خود را مدافع فلسفه طبيعي يونان مي دانست و كنكاش در آن با خطرات زيادي همراه بود، انديشمندان كنجكاو بيشتر به رياضيات مي پرداختند، زيرا كليسا نسبت به آن حساسيت نشان نمي داد. بنابراين رياضيات نسبت به فيزيك از پيشرفت بيشتري برخوردار بود. يكي از شاخه هاي مهم رياضيات هندسه بود كه آن هم در هندسه ي اقليدسي خلاصه مي شد.
در هندسه ي اقليدسي يكسري مفاهيم اوليه نظير خط و نقطه تعريف شده بود و پنچ اصل را به عنوان بديهيات پذيرفته بودند و ساير قضايا را با استفاده از اين اصول استنتاج مي كردند. اما اصل پنجم چندان بديهي به نظر نمي رسيد. بنابر اصل پنجم اقليدس از يك نقطه خارج از يك خط، يك خط و تنها يك خط مي توان موازي با خط مفروض رسم كرد. برخي از رياضيدانان مدعي بودند كه اين اصل را مي توان به عنوان يك قضيه ثابت كرد. در اين راه بسياري از رياضيدانان تلاش زيادي كردند و نتيجه نگرفتند. خيام ضمن جستجوي راهي براي اثبات “اصل توازي” مبتكر مفهوم عميقي در هندسه شد. در تلاش براي اثبات اين اصل، خيام گزاره هايي را بيان كرد كه كاملا مطابق گزاره هايي بود كه چند قرن بعد توسط واليس و ساكري رياضيدانان اروپايي بيان شد و راه را براي ظهور هندسه هاي نااقليدسي در قرن نوزدهم هموار كرد. سرانجام و پس از دو هزار سال اصولي متفاوت با آن بيان كردند و هندسه هاي نااقليدسي شكل گرفت. بدين ترتيب علاوه بر فلسفه ي طبيعي رياضيات نيز از انحصار يوناني خارج و در مسيري جديد قرار گرفت و آزاد انديشي در رياضيات آغاز گرديد.
۱-۵ اصطلاحات بنيادي رياضيات
طي قرنهاي متمادي رياضيدانان اشياء و موضوع هاي مورد مطلعه ي خود از قبيل نقطه و خط و عدد را همچون كميت هايي در نظر مي گرفتند كه در نفس خويش وجود دارند. اين موجودات همواره همه ي كوششهاي را كه براي تعريف و توصيف شايسته ي آنان انجام مي شد را با شكست مواجه مي ساختند. بتدريج اين نكته بر رياضيدانان قرن نوزدهم آشكار گرديد كه تعيين مفهوم اين موجودات نمي تواند در داخل رياضيات معنايي داشته باشد. حتي اگر اصولاً داراي معنايي باشند.
بنابراين، اينكه اعداد، نقطه و خط در واقع چه هستند در علوم رياضي نه قابل بحث است و نه احتياجي به اين بحث هست. يك وقت براتراند راسل گفته بود كه رياضيات موضوعي است كه در آن نه مي دانيم از چه سخن مي گوييم و نه مي دانيم آنچه كه مي گوييم درست است.
دليل آن اين است كه برخي از اصطلاحات اوليه نظير نقطه، خط و صفحه تعريف نشده اند و ممكن است به جاي آنها اصطلاحات ديگري بگذاريم بي آنكه در درستي نتايج تاثيري داشته باشد. مثلاً مي توانيم به جاي آنكه بگوييم دو نقطه فقط يك خط را مشخص مي كند، مي توانيم بگوييم دو آلفا يك بتا را مشخص مي كند. با وجود تغييري كه در اصطلاحات داديم، باز هم اثبات همه ي قضاياي ما معتبر خواهد ماند، زيرا كه دليل هاي درست به شكل نمودار بسته نيستند، بلكه فقط به اصول موضوع كه وضع شده اند و قواعد منطق بستگي دارند.
بنابراين، رياضيات تمريني است كاملاً صوري براي استخراج برخي نتايج از بعضي مقدمات صوري. رياضيات احكامي مي سازند به صورت هرگاه چنين باشد، آنگاه چنان خواهد شد و اساساً در آن صحبتي از معني فرضها يا راست بودن آنها نيست. اين ديدگاه (صوريگرايي) با عقيده ي كهن تري كه رياضيات را حقيقت محض مي پنداشت و كشف هندسه هاي نااقليدسي بناي آن را درهم ريخت، جدايي اساسي دارد. اين كشف اثر آزادي بخشي بر رياضيدانان داشت.
۲-۵ اشكالات وارد بر هندسه اقليدسي
هندسه ي اقليدسي بر اساس پنچ اصل موضوع زير شكل گرفت:
اصل اول - از هر نقطه مي توان خط مستقيمي به هر نقطه ي ديگر كشيد.
اصل دوم - هر پاره خط مستقيم را مي توان روي همان خط به طور نامحدود امتداد داد.
اصل سوم - مي توان دايره اي با هر نقطه دلخواه به عنوان مركز آن و با شعاعي مساوي هر پاره خط رسم كرد.
اصل چهارم - همه ي زواياي قائمه با هم مساوي اند.
اصل پنجم - از يك نقطه خارج يك خط، يك خط و و تنها يك خط مي توان موازي با خط مفروض رسم كرد.
اصل پنجم اقليدس كه ايجاز ساير اصول را نداشت، به هيچوجه واجد صفت بديهي نبود. در واقع اين اصل بيشتر به يك قضيه شباهت داشت تا به يك اصل. بنابراين طبيعي بود كه لزوم واقعي آن به عنوان يك اصل مورد سئوال قرار گيرد. زيرا چنين تصور مي شد كه شايد بتوان آن را به عنوان يك قضيه نه اصل از ساير اصول استخراج كرد، يا حداقل به جاي آن مي توان معادل قابل قبول تري قرار داد.
در طول تاريخ رياضيدانان بسياري از جمله، خواجه نصيرالدين طوسي، جان واليس، لژاندر، فوركوش بويوئي و … تلاش كردند اصل پنجم اقليدس را با استفاده از ساير اصول نتيجه بگيرنر و آن را به عنوان يك قضيه اثبات كنند. اما تمام تلاشها بي نتيجه بود و در اثبات دچار خطا مي شدند و به نوعي همين اصل را در اثباط خود به كار مي بردند. دلامبر اين وضع را افتضاح هندسه ناميد.
يانوش بويوئي يكي از رياضيدانان جواني بود كه در اين را تلاش مي كرد. پدر وي نيز رياضيداني بود كه سالها در اين اين مسير تلاش كرده بود .
و طي نامه اي به پسرش نوشت: تو ديگر نبايد براي گام نهادن در راه توازي ها تلاش كني، من پيچ و خم اين راه را از اول تا آخر مي شناسم. اين شب بي پايان همه روشنايي و شادماني زندگي مرا به كام نابودي فرو برده است، التماس مي كنم دانش موازيها را رها كني.
ولي يانوش جوان از اخطار پدير نهرسيد، زيرا كه انديشه ي كاملاً تازه اي را در سر مي پروراند. او فرض كرد نقيض اصل توازي اقليدس، حكم بي معني اي نيست. وي در سال ۱۸۲۳ پدرش را محرمانه در جريان كشف خود قرار داد و در سال ۱۸۳۱ اكتشافات خود را به صورت ضميمه در كتاب تنتامن پدرش منتشر كرد و نسخه اي از آن را براي گائوس فرستاد. بعد معلوم شد كه گائوس خود مستقلاً آن را كشف كرده است.
بعدها مشخص شد كه لباچفسكي در سال ۱۸۲۹ كشفيات خود را در باره هندسه نااقليدسي در بولتن كازان، دو سال قبل از بوئي منتشر كرده است. و بدين ترتيب كشف هندسه هاي نااقليدسي به نام بويوئي و لباچفسكي ثبت گرديد.
۳-۵ هندسه هاي نا اقليدسي
اساساً هندسه نااقليدسي چيست؟ هر هندسه اي غير از اقليدسي را نا اقليدسي مي نامند. از اين گونه هندسه ها تا به حال زياد شناخته شده است. اختلاف بين هندسه هاي نا اقليدسي و اقليدسي تنها در اصل توازي است. در هندسه اقليدسي به ازاي هر خط و هر نقطه نا واقع بر آن يك خط مي توان موازي با آن رسم كرد.
نقيض اين اصل را به دو صورت مي توان در نظر گرفت. تعداد خطوط موازي كه از يك نقطه نا واقع بر آن، مي توان رسم كرد، بيش از يكي است. و يا اصلاً خطوط موازي وجود ندارند. با توجه به اين دو نقيض، هندسه هاي نا اقليدسي را مي توان به دو گروه تقسيم كرد.
يك - هندسه هاي هذلولوي
هندسه هاي هذلولوي توسط بويوئي و لباچفسكي بطور مستقل و همزمان كشف گرديد.
اصل توازي هندسه هذلولوي - از يك خط و يك نقطه ي نا واقع بر آن دست كم دو خط موازي با خط مفروض مي توان رسم كرد.
دو - هندسه هاي بيضوي
در سال ۱۸۵۴ فريدريش برنهارد ريمان نشان داد كه اگر نامتناهي بودن خط مستقيم كنار گذاشته شود و صرفاً بي كرانگي آن مورد پذيرش واقع شود، آنگاه با چند جرح و تعديل جزئي اصول موضوعه ديگر، هندسه سازگار نااقليدسي ديگري را مي توان به دست آورد. پس از اين تغييرات اصل توازي هندسه بيضوي بصورت زير ارائه گرديد.
اصل توازي هندسه بيضوي - از يك نقطه ناواقع بر يك خط نمي توان خطي به موازات خط مفروض رسم كرد.
يعني در هندسه بيضوي، خطوط موازي وجود ندارد. با تجسم سطح يك كره مي توان سطحي شبيه سطح بيضوي در نظر گرفت. اين سطح كروي را مشابه يك صفحه در نظر مي گيرند. در اينجا خطوط با دايره هاي عظميه كره نمايش داده مي شوند. بنابراين خط ژئودزيك يا مساحتي در هندسه بيضوي بخشي از يك دايره عظيمه است.
در هندسه بيضوي مجموع زواياي يك مثلث بيشتر از ۱۸۰ درجه است. در هندسه بيضوي با حركت از يك نقطه و پيمودن يك خط مستقيم در آن صفحه، مي توان به نقطه ي اول باز گشت. همچنين مي توان ديد كه در هندسه بيضوي نسبت محيط يك دايره به قطر آن همواره كمتر از عدد پي است.
۴-۵ انحناي سطح يا انحناي گائوسي
اگر خط را راست فرض كنيم نه خميده، چنانچه ناگزير باشيم يك انحناي عددي k به خطي نسبت دهيم براي خط راست خواهيم داشت k=o انحناي يك دايره به شعاع r برابر است با k=۱/r.
تعريف مي كنند. همچنين منحني هموار، منحني اي است كه مماس بر هر نقطه اش به بطور پيوسته تغيير كند. به عبارت ديگر منحني هموار يعني در تمام نقاطش مشتق پذير باشد.
براي به دست آوردن انحناي يك منحني در يك نقطه، دايره بوسان آنرا در آن نقطه رسم كرده، انحناي منحني در آن نقطه برابر با انحناي دايره ي بوسان در آن نقطه است. دايره بوسان در يك نقطه از منحني، دايره اي است كه در آن نقطه با منحني بيشترين تماس را دارد. توجه شود كه براي خط راست شعاع دايره بوسان آن در هر نقطه واقع بر آن بينهايت است.
براي تعيين انحناي يك سطح در يك نقطه، دو خط متقاطع مساحتي در دو جهت اصلي در آن نقطه انتخاب كرده و انحناي اين دو خط را در آن نقاط تعيين مي كنيم. فرض كنيم انحناي اين دو خط
k۱=۱/R۱ and k۲=۱/R۲
باشند. آنگاه انحناي سطح در آن نقطه برابر است با حاصلضرب اين دو انحنا، يعني :
k=۱/R۱R۲
انحناي صفحه ي اقليدسي صفر است. همچنين انحناي استوانه صفر است:
k=o
براي سطح هذلولوي همواره انحناي سطح منفي است :
k<>
براي سطح بيضوي همواره انحنا مثبت است :
k>o
در جدول زير هر سه هندسه ها با يكديگر مقايسه شده اند:
۴-۶ مفهوم و درك شهودي انحناي فضا
سئوال اساسي اين است كه كدام يك از اين هندسه هاي اقليدسي يا نا اقليدسي درست است؟
پاسخ صريح و روشن اين است كه بايد انحناي يك سطح را تعيين كنيم تا مشخص شود كدام يك درست است. بهترين دانشي كا مي تواند در شناخت نوع هندسه ي يك سطح مورد استفاده و استناد قرار گيرد، فيزيك است. يك صفحه ي كاغذ برداريد و در روي آن دو خط متقاطع رسم كنيد. سپس انحناي اين خطوط را در آن نقطه تعيين كرده و با توجه به تعريف انحناي سطح حاصلضرب آن را به دست مي آوريم. اگر مقدار انحنا برابر صفر شد، صفحه اقليدسي است، اگر منفي شد مي گوييم صفحه هذلولوي است و در صورتي كه مثبت شود، ادعا مي كنيم كه صفحه بيضوي است .
در كارهاي معمولي مهندسي نظير ايجاد ساختمان يا ساختن يك سد بر روي رودخانه، انحناي سطح مورد نظر برابر صفر است، به همين دليل در طول تلريخ مهندسين همواره از هندسه اقليدسي استفاده كرده اند و با هيچگونه مشكلي هم مواجه نشدند. يا براي نقشه برداري از سطح يك كشور اصول هندسه ي اقليدسي را بكار مي برند و فراز و نشيب نقاط مختلف آن را مشخص مي كنند. در اين محاسبات ما مي توانيم از خطكش هايي كه در آزمايشگاه يا كارخانه ها ساخته مي شود، استفاده كنيم. حال سئوال اين است كه اگر خطكش مورد استفاده ي ما تحت تاثير شرايط محيطي قرار بگيرد چه بايد كرد؟ اما مي دانيم از هر ماده اي كه براي ساختن خطكش استفاده كنيم، شرايط فيزيكي محيط بر روي آن اثر مي گذارد. البته با توجه با تاثير محيط بر روي خطكش ما تلاش مي كنيم از بهترين ماده ي ممكن استفاده كنيم. بهمين دليل چوب از لاستيك بهتر است و آهن بهتر از چوب است.
اما براي مصافتهاي دور نظير فواصل نجومي از چه خطكشي (متري) مي توانيم استفاده كنيم؟ طبيعي است كه در اينجا هيچ خطكشي وجود ندارد كه بتوانيم با استفاده از آن فاصله ي بين زمين و ماه يا ستارگان را اندازه بگيريم. بنابراين بايد به ساير امكاناتي توجه كنيم كه در عمل قابل استفاده است. اما در اينجا چه امكاناتي داريم؟ بهترين ابزار شناخته شده امواج الكترومغناطيسي است. اگر مسير نور در فضا خط مستقيم باشد، در اينصورت با جرت مي توانيم ادعا كنيم كه فضا اقليدسي است. براي پي بردن به نوع انحناي فضا بايد مسير پرتو نوري را مورد بررسي قرار دهيم .
اما تجربه نشان مي دهد كه مسير نور هنگام عبور از كنار ماده يعني زماني كه از يك ميدان گرانشي عبور مي كند، خط مستقيم نيست، بلكه منحني است. بنابراين فضاي اطراف اجسام اقليدسي نيست. به عبارت ديگر ساختار هندسي فضا نااقليدسي است.
هندسه نااقليدسي و انحناي فضا
علومي كه از يونان باستان توسط انديشمندان اسلامي محافظت و تكميل شد، از قرون يازدهم ميلادي به بعد به اروپا منتقل شد، بيشتر شامل رياضي و فلسفه ي طبيعي بود. فلسفه ي طبيعي توسط كوپرنيك، برونو، كپلر و گاليله به چالش كشيده شد و از آن ميان فيزيك نيوتني بيرون آمد. چون كليسا خود را مدافع فلسفه طبيعي يونان مي دانست و كنكاش در آن با خطرات زيادي همراه بود، انديشمندان كنجكاو بيشتر به رياضيات مي پرداختند، زيرا كليسا نسبت به آن حساسيت نشان نمي داد. بنابراين رياضيات نسبت به فيزيك از پيشرفت بيشتري برخوردار بود. يكي از شاخه هاي مهم رياضيات هندسه بود كه آن هم در هندسه ي اقليدسي خلاصه مي شد.
در هندسه ي اقليدسي يكسري مفاهيم اوليه نظير خط و نقطه تعريف شده بود و پنچ اصل را به عنوان بديهيات پذيرفته بودند و ساير قضايا را با استفاده از اين اصول استنتاج مي كردند. اما اصل پنجم چندان بديهي به نظر نمي رسيد. بنابر اصل پنجم اقليدس از يك نقطه خارج از يك خط، يك خط و تنها يك خط مي توان موازي با خط مفروض رسم كرد. برخي از رياضيدانان مدعي بودند كه اين اصل را مي توان به عنوان يك قضيه ثابت كرد. در اين راه بسياري از رياضيدانان تلاش زيادي كردند و نتيجه نگرفتند. خيام ضمن جستجوي راهي براي اثبات “اصل توازي” مبتكر مفهوم عميقي در هندسه شد. در تلاش براي اثبات اين اصل، خيام گزاره هايي را بيان كرد كه كاملا مطابق گزاره هايي بود كه چند قرن بعد توسط واليس و ساكري رياضيدانان اروپايي بيان شد و راه را براي ظهور هندسه هاي نااقليدسي در قرن نوزدهم هموار كرد. سرانجام و پس از دو هزار سال اصولي متفاوت با آن بيان كردند و هندسه هاي نااقليدسي شكل گرفت. بدين ترتيب علاوه بر فلسفه ي طبيعي رياضيات نيز از انحصار يوناني خارج و در مسيري جديد قرار گرفت و آزاد انديشي در رياضيات آغاز گرديد.
۱-۵ اصطلاحات بنيادي رياضيات
طي قرنهاي متمادي رياضيدانان اشياء و موضوع هاي مورد مطلعه ي خود از قبيل نقطه و خط و عدد را همچون كميت هايي در نظر مي گرفتند كه در نفس خويش وجود دارند. اين موجودات همواره همه ي كوششهاي را كه براي تعريف و توصيف شايسته ي آنان انجام مي شد را با شكست مواجه مي ساختند. بتدريج اين نكته بر رياضيدانان قرن نوزدهم آشكار گرديد كه تعيين مفهوم اين موجودات نمي تواند در داخل رياضيات معنايي داشته باشد. حتي اگر اصولاً داراي معنايي باشند.
بنابراين، اينكه اعداد، نقطه و خط در واقع چه هستند در علوم رياضي نه قابل بحث است و نه احتياجي به اين بحث هست. يك وقت براتراند راسل گفته بود كه رياضيات موضوعي است كه در آن نه مي دانيم از چه سخن مي گوييم و نه مي دانيم آنچه كه مي گوييم درست است.
دليل آن اين است كه برخي از اصطلاحات اوليه نظير نقطه، خط و صفحه تعريف نشده اند و ممكن است به جاي آنها اصطلاحات ديگري بگذاريم بي آنكه در درستي نتايج تاثيري داشته باشد. مثلاً مي توانيم به جاي آنكه بگوييم دو نقطه فقط يك خط را مشخص مي كند، مي توانيم بگوييم دو آلفا يك بتا را مشخص مي كند. با وجود تغييري كه در اصطلاحات داديم، باز هم اثبات همه ي قضاياي ما معتبر خواهد ماند، زيرا كه دليل هاي درست به شكل نمودار بسته نيستند، بلكه فقط به اصول موضوع كه وضع شده اند و قواعد منطق بستگي دارند.
بنابراين، رياضيات تمريني است كاملاً صوري براي استخراج برخي نتايج از بعضي مقدمات صوري. رياضيات احكامي مي سازند به صورت هرگاه چنين باشد، آنگاه چنان خواهد شد و اساساً در آن صحبتي از معني فرضها يا راست بودن آنها نيست. اين ديدگاه (صوريگرايي) با عقيده ي كهن تري كه رياضيات را حقيقت محض مي پنداشت و كشف هندسه هاي نااقليدسي بناي آن را درهم ريخت، جدايي اساسي دارد. اين كشف اثر آزادي بخشي بر رياضيدانان داشت.
۲-۵ اشكالات وارد بر هندسه اقليدسي
هندسه ي اقليدسي بر اساس پنچ اصل موضوع زير شكل گرفت:
اصل اول - از هر نقطه مي توان خط مستقيمي به هر نقطه ي ديگر كشيد.
اصل دوم - هر پاره خط مستقيم را مي توان روي همان خط به طور نامحدود امتداد داد.
اصل سوم - مي توان دايره اي با هر نقطه دلخواه به عنوان مركز آن و با شعاعي مساوي هر پاره خط رسم كرد.
اصل چهارم - همه ي زواياي قائمه با هم مساوي اند.
اصل پنجم - از يك نقطه خارج يك خط، يك خط و و تنها يك خط مي توان موازي با خط مفروض رسم كرد.
اصل پنجم اقليدس كه ايجاز ساير اصول را نداشت، به هيچوجه واجد صفت بديهي نبود. در واقع اين اصل بيشتر به يك قضيه شباهت داشت تا به يك اصل. بنابراين طبيعي بود كه لزوم واقعي آن به عنوان يك اصل مورد سئوال قرار گيرد. زيرا چنين تصور مي شد كه شايد بتوان آن را به عنوان يك قضيه نه اصل از ساير اصول استخراج كرد، يا حداقل به جاي آن مي توان معادل قابل قبول تري قرار داد.
در طول تاريخ رياضيدانان بسياري از جمله، خواجه نصيرالدين طوسي، جان واليس، لژاندر، فوركوش بويوئي و … تلاش كردند اصل پنجم اقليدس را با استفاده از ساير اصول نتيجه بگيرنر و آن را به عنوان يك قضيه اثبات كنند. اما تمام تلاشها بي نتيجه بود و در اثبات دچار خطا مي شدند و به نوعي همين اصل را در اثباط خود به كار مي بردند. دلامبر اين وضع را افتضاح هندسه ناميد.
يانوش بويوئي يكي از رياضيدانان جواني بود كه در اين را تلاش مي كرد. پدر وي نيز رياضيداني بود كه سالها در اين اين مسير تلاش كرده بود .
و طي نامه اي به پسرش نوشت: تو ديگر نبايد براي گام نهادن در راه توازي ها تلاش كني، من پيچ و خم اين راه را از اول تا آخر مي شناسم. اين شب بي پايان همه روشنايي و شادماني زندگي مرا به كام نابودي فرو برده است، التماس مي كنم دانش موازيها را رها كني.
ولي يانوش جوان از اخطار پدير نهرسيد، زيرا كه انديشه ي كاملاً تازه اي را در سر مي پروراند. او فرض كرد نقيض اصل توازي اقليدس، حكم بي معني اي نيست. وي در سال ۱۸۲۳ پدرش را محرمانه در جريان كشف خود قرار داد و در سال ۱۸۳۱ اكتشافات خود را به صورت ضميمه در كتاب تنتامن پدرش منتشر كرد و نسخه اي از آن را براي گائوس فرستاد. بعد معلوم شد كه گائوس خود مستقلاً آن را كشف كرده است.
بعدها مشخص شد كه لباچفسكي در سال ۱۸۲۹ كشفيات خود را در باره هندسه نااقليدسي در بولتن كازان، دو سال قبل از بوئي منتشر كرده است. و بدين ترتيب كشف هندسه هاي نااقليدسي به نام بويوئي و لباچفسكي ثبت گرديد.
۳-۵ هندسه هاي نا اقليدسي
اساساً هندسه نااقليدسي چيست؟ هر هندسه اي غير از اقليدسي را نا اقليدسي مي نامند. از اين گونه هندسه ها تا به حال زياد شناخته شده است. اختلاف بين هندسه هاي نا اقليدسي و اقليدسي تنها در اصل توازي است. در هندسه اقليدسي به ازاي هر خط و هر نقطه نا واقع بر آن يك خط مي توان موازي با آن رسم كرد.
نقيض اين اصل را به دو صورت مي توان در نظر گرفت. تعداد خطوط موازي كه از يك نقطه نا واقع بر آن، مي توان رسم كرد، بيش از يكي است. و يا اصلاً خطوط موازي وجود ندارند. با توجه به اين دو نقيض، هندسه هاي نا اقليدسي را مي توان به دو گروه تقسيم كرد.
يك - هندسه هاي هذلولوي
هندسه هاي هذلولوي توسط بويوئي و لباچفسكي بطور مستقل و همزمان كشف گرديد.
اصل توازي هندسه هذلولوي - از يك خط و يك نقطه ي نا واقع بر آن دست كم دو خط موازي با خط مفروض مي توان رسم كرد.
دو - هندسه هاي بيضوي
در سال ۱۸۵۴ فريدريش برنهارد ريمان نشان داد كه اگر نامتناهي بودن خط مستقيم كنار گذاشته شود و صرفاً بي كرانگي آن مورد پذيرش واقع شود، آنگاه با چند جرح و تعديل جزئي اصول موضوعه ديگر، هندسه سازگار نااقليدسي ديگري را مي توان به دست آورد. پس از اين تغييرات اصل توازي هندسه بيضوي بصورت زير ارائه گرديد.
اصل توازي هندسه بيضوي - از يك نقطه ناواقع بر يك خط نمي توان خطي به موازات خط مفروض رسم كرد.
يعني در هندسه بيضوي، خطوط موازي وجود ندارد. با تجسم سطح يك كره مي توان سطحي شبيه سطح بيضوي در نظر گرفت. اين سطح كروي را مشابه يك صفحه در نظر مي گيرند. در اينجا خطوط با دايره هاي عظميه كره نمايش داده مي شوند. بنابراين خط ژئودزيك يا مساحتي در هندسه بيضوي بخشي از يك دايره عظيمه است.
در هندسه بيضوي مجموع زواياي يك مثلث بيشتر از ۱۸۰ درجه است. در هندسه بيضوي با حركت از يك نقطه و پيمودن يك خط مستقيم در آن صفحه، مي توان به نقطه ي اول باز گشت. همچنين مي توان ديد كه در هندسه بيضوي نسبت محيط يك دايره به قطر آن همواره كمتر از عدد پي است.
۴-۵ انحناي سطح يا انحناي گائوسي
اگر خط را راست فرض كنيم نه خميده، چنانچه ناگزير باشيم يك انحناي عددي k به خطي نسبت دهيم براي خط راست خواهيم داشت k=o انحناي يك دايره به شعاع r برابر است با k=۱/r.
تعريف مي كنند. همچنين منحني هموار، منحني اي است كه مماس بر هر نقطه اش به بطور پيوسته تغيير كند. به عبارت ديگر منحني هموار يعني در تمام نقاطش مشتق پذير باشد.
براي به دست آوردن انحناي يك منحني در يك نقطه، دايره بوسان آنرا در آن نقطه رسم كرده، انحناي منحني در آن نقطه برابر با انحناي دايره ي بوسان در آن نقطه است. دايره بوسان در يك نقطه از منحني، دايره اي است كه در آن نقطه با منحني بيشترين تماس را دارد. توجه شود كه براي خط راست شعاع دايره بوسان آن در هر نقطه واقع بر آن بينهايت است.
براي تعيين انحناي يك سطح در يك نقطه، دو خط متقاطع مساحتي در دو جهت اصلي در آن نقطه انتخاب كرده و انحناي اين دو خط را در آن نقاط تعيين مي كنيم. فرض كنيم انحناي اين دو خط
k۱=۱/R۱ and k۲=۱/R۲
باشند. آنگاه انحناي سطح در آن نقطه برابر است با حاصلضرب اين دو انحنا، يعني :
k=۱/R۱R۲
انحناي صفحه ي اقليدسي صفر است. همچنين انحناي استوانه صفر است:
k=o
براي سطح هذلولوي همواره انحناي سطح منفي است :
k<>
براي سطح بيضوي همواره انحنا مثبت است :
k>o
در جدول زير هر سه هندسه ها با يكديگر مقايسه شده اند:
| نوع هندسه | تعداد خطوط موازي | مجموع زواياي مثللث | نسبت محيط به قطر دايره | اندازه انحنا |
| اقليدسي | يك | ۱۸۰ | عدد پي | صفر |
| هذلولوي | بينهايت | < 180 | > عدد پي | منفي |
| بيضوي | صفر | > ۱۸۰ | < عدد پي | مثبت |
۴-۶ مفهوم و درك شهودي انحناي فضا
سئوال اساسي اين است كه كدام يك از اين هندسه هاي اقليدسي يا نا اقليدسي درست است؟
پاسخ صريح و روشن اين است كه بايد انحناي يك سطح را تعيين كنيم تا مشخص شود كدام يك درست است. بهترين دانشي كا مي تواند در شناخت نوع هندسه ي يك سطح مورد استفاده و استناد قرار گيرد، فيزيك است. يك صفحه ي كاغذ برداريد و در روي آن دو خط متقاطع رسم كنيد. سپس انحناي اين خطوط را در آن نقطه تعيين كرده و با توجه به تعريف انحناي سطح حاصلضرب آن را به دست مي آوريم. اگر مقدار انحنا برابر صفر شد، صفحه اقليدسي است، اگر منفي شد مي گوييم صفحه هذلولوي است و در صورتي كه مثبت شود، ادعا مي كنيم كه صفحه بيضوي است .
در كارهاي معمولي مهندسي نظير ايجاد ساختمان يا ساختن يك سد بر روي رودخانه، انحناي سطح مورد نظر برابر صفر است، به همين دليل در طول تلريخ مهندسين همواره از هندسه اقليدسي استفاده كرده اند و با هيچگونه مشكلي هم مواجه نشدند. يا براي نقشه برداري از سطح يك كشور اصول هندسه ي اقليدسي را بكار مي برند و فراز و نشيب نقاط مختلف آن را مشخص مي كنند. در اين محاسبات ما مي توانيم از خطكش هايي كه در آزمايشگاه يا كارخانه ها ساخته مي شود، استفاده كنيم. حال سئوال اين است كه اگر خطكش مورد استفاده ي ما تحت تاثير شرايط محيطي قرار بگيرد چه بايد كرد؟ اما مي دانيم از هر ماده اي كه براي ساختن خطكش استفاده كنيم، شرايط فيزيكي محيط بر روي آن اثر مي گذارد. البته با توجه با تاثير محيط بر روي خطكش ما تلاش مي كنيم از بهترين ماده ي ممكن استفاده كنيم. بهمين دليل چوب از لاستيك بهتر است و آهن بهتر از چوب است.
اما براي مصافتهاي دور نظير فواصل نجومي از چه خطكشي (متري) مي توانيم استفاده كنيم؟ طبيعي است كه در اينجا هيچ خطكشي وجود ندارد كه بتوانيم با استفاده از آن فاصله ي بين زمين و ماه يا ستارگان را اندازه بگيريم. بنابراين بايد به ساير امكاناتي توجه كنيم كه در عمل قابل استفاده است. اما در اينجا چه امكاناتي داريم؟ بهترين ابزار شناخته شده امواج الكترومغناطيسي است. اگر مسير نور در فضا خط مستقيم باشد، در اينصورت با جرت مي توانيم ادعا كنيم كه فضا اقليدسي است. براي پي بردن به نوع انحناي فضا بايد مسير پرتو نوري را مورد بررسي قرار دهيم .
اما تجربه نشان مي دهد كه مسير نور هنگام عبور از كنار ماده يعني زماني كه از يك ميدان گرانشي عبور مي كند، خط مستقيم نيست، بلكه منحني است. بنابراين فضاي اطراف اجسام اقليدسي نيست. به عبارت ديگر ساختار هندسي فضا نااقليدسي است.
داداشی توکه اولش رفتی فوق دکتراشو بیان کردی !!!! دستت درد نکنه ولی فکر ما رو بکن ! شما لطف کن قرار بود از پایه ، پایه یعنی از دوران دبیرستان پیش میریم تا مسئله ای واسه کسی نباشه ، ولی بازم ممنون که تنهام نذاشتی
دبیرستان شما خیلی کار درست بوده ، باور کن در دوران دبیرستان نتونستم حتی یک چیز بجز کتاب درسی یاد بگیریم . واقعا متاسفم ، حالا تو کمک کن اینجا بشه دبیرستان شما ، ولی با این فرق که از این به بعد شما آقا معلم . اجازه !!!
من تو دوران دبیرستان اصلا درس نمیخوندم و هیچی بلد نیستم
حالا کمک میکنیم قوی شه پایه مون
از کجا شروع کنیم؟
من پایه ی فیزیکم هستم ( از مکانیک شروع کنیم و با زمانبندی مشترک پیش بریم و مشکلی داشتیم مطرح کنیم و بحث کنیم و چندتا از سوالای جالبو مطرح کنیم و حل کنیم و ...)
قربون معرفتت من سرفصل کتاب فیزیک نگاه می کنم بعد بهتون خبر می دم سعی می کنم بهترین و قوی ترین تاپیک بسازم البته البته با کمک صددرصد شما ، یک لطفی کن واسه بقیه بچه های مشتاق اطلاع رسانی کن . پیشاپیش از مساعدت شما کمال تشکر دارم
یکاهای اصلی و فرعی
بعضی کمیتهای اصلی فیزیک عبارتند از طول، جرم و زمان و یکاهای اصلی، یکاهای این کمیتهای اصلی اند.
کمیتهای فرعی مثل مساحت، حجم، سرعت و ... با استفاده یا رابطه هایی با کمیتهای اصلی به دست می آیند. یکای کمیتهای فرعی هم با استفاده از این روابط تعریف می شود. مثلاً مسافت که از حاصل ضرب دو طول به دست می آید m[SUP]2 [/SUP][SUP] = [/SUP]m×m (متر مربع) می باشد.
یکای مناسب برای کمیتهای خیلی بزرگ یا خیلی کوچک
یکاهای کوچکتر و یا بزرگتر را توسط پیشوندی که به یکای مربوط اضافه می شود.
را به صد قسمت مساوی تقسیم کنیم هر قسمت یک سانتیمتر است. جدول زیر مربوط به این پیشوندها است.
نماد گذاری علمی
در نماد گذاری علمی هر مقدار را به صورت حاصل ضرب عددی بین ۱ و ۱۰ و توان صحیحی از ۱۰ می نویسند. مثال:
10[SUP]6[/SUP] × 63/5= 5630000
%820 = 8/2 * 10[SUP]-2[/SUP]
وسایل اندازه گیری
وسایل اندازه گیری با توجه به کمیت مورد اندازه گیری انتخاب و طراحی می شوند. مثلاً برای اندازه گیری طول و عرض یک اتاق از متر نواری و برای اندازه گیری طول و عرض یک کتاب از یک خط کش استفاده می شود. برای اندازه گیری جرم جسم از ترازو، برای اندازه گیری زمان از ساعت و برای اندازه گیری حجم مایعها از پیمانه ها یا ظرفهای مدرج استفاده می شود.
دقت اندازه گیری
کمترین مقداری را که یک وسیله می تواند اندازه بگیرد دقت اندازه گیری با آن وسیله می نامند. به عنوان مثال دقت اندازه گیری یک خط کش معمولی در حد میلی متر است و برای اندازه گیری طول کمتر از میلی متر باید از وسیله ای که دقت آن بیشتر باشد مثل کولین یا ریز سنج استفاده کرد.
کمیتهای فیزیکی
کمیتهای فیزیکی دو دسته اند: نرده ای و برداری
کمیتهای نرده ای: این کمیتها با معلوم شدن مقدارشان معرفی و مشخص می شوند مثل حجم سطح، جرم، زمان، طول، انرژی، چگالی و ... این کمیتها از قاعده های متداول در حساب پیروی می کنند.
کمیتهای برداری: این کمیتها علاوه بر بزرگی (مقدار)، جهت (راستا و سو) دارند و از قاعده جمع برداری پیروی می کنند.
بعضی کمیتهای اصلی فیزیک عبارتند از طول، جرم و زمان و یکاهای اصلی، یکاهای این کمیتهای اصلی اند.
| یکاهای اصلی | کمیتهای اصلی |
| (M) متر | طول |
| (Kg) کیلوگرم | جرم |
| (s) ثانیه | زمان |
کمیتهای فرعی مثل مساحت، حجم، سرعت و ... با استفاده یا رابطه هایی با کمیتهای اصلی به دست می آیند. یکای کمیتهای فرعی هم با استفاده از این روابط تعریف می شود. مثلاً مسافت که از حاصل ضرب دو طول به دست می آید m[SUP]2 [/SUP][SUP] = [/SUP]m×m (متر مربع) می باشد.
یکای مناسب برای کمیتهای خیلی بزرگ یا خیلی کوچک
یکاهای کوچکتر و یا بزرگتر را توسط پیشوندی که به یکای مربوط اضافه می شود.
| نامگذاری می کنند. مثلاًً از پیشوند «سانتی» برای |
| استفاده می شود. یعنی اگر یک متر |
| پیشوند | مضرب | نماد | پیشوند | مضرب | نماد |
| دسی | 1/10 = 10[SUP]-1[/SUP] | d | دکا | 10 | da |
| سانتی | 1/100 = 10[SUP]-2[/SUP] | c | هکتو | 100 | h |
| میلی | 1/1000 = 10[SUP]-3[/SUP] | m | کیلو | 1000 | k |
| میکرو | 1/10[SUP]6 [/SUP]= 10[SUP]-6[/SUP] | m | مگا | 10[SUP]6[/SUP] | M |
| نانو | 1/10[SUP]9[/SUP]=10[SUP]-9[/SUP] | n | گیگا | 10[SUP]9[/SUP] | G |
| پیکو | 1/10[SUP]12[/SUP] =10[SUP]-12[/SUP] | p | ترا | 10[SUP]12[/SUP] | T |
نماد گذاری علمی
در نماد گذاری علمی هر مقدار را به صورت حاصل ضرب عددی بین ۱ و ۱۰ و توان صحیحی از ۱۰ می نویسند. مثال:
10[SUP]6[/SUP] × 63/5= 5630000
%820 = 8/2 * 10[SUP]-2[/SUP]
وسایل اندازه گیری
وسایل اندازه گیری با توجه به کمیت مورد اندازه گیری انتخاب و طراحی می شوند. مثلاً برای اندازه گیری طول و عرض یک اتاق از متر نواری و برای اندازه گیری طول و عرض یک کتاب از یک خط کش استفاده می شود. برای اندازه گیری جرم جسم از ترازو، برای اندازه گیری زمان از ساعت و برای اندازه گیری حجم مایعها از پیمانه ها یا ظرفهای مدرج استفاده می شود.
دقت اندازه گیری
کمترین مقداری را که یک وسیله می تواند اندازه بگیرد دقت اندازه گیری با آن وسیله می نامند. به عنوان مثال دقت اندازه گیری یک خط کش معمولی در حد میلی متر است و برای اندازه گیری طول کمتر از میلی متر باید از وسیله ای که دقت آن بیشتر باشد مثل کولین یا ریز سنج استفاده کرد.
کمیتهای فیزیکی
کمیتهای فیزیکی دو دسته اند: نرده ای و برداری
کمیتهای نرده ای: این کمیتها با معلوم شدن مقدارشان معرفی و مشخص می شوند مثل حجم سطح، جرم، زمان، طول، انرژی، چگالی و ... این کمیتها از قاعده های متداول در حساب پیروی می کنند.
کمیتهای برداری: این کمیتها علاوه بر بزرگی (مقدار)، جهت (راستا و سو) دارند و از قاعده جمع برداری پیروی می کنند.
بردارهایی که اندازه جهت آنها یکسان است و راستاهای موازی دارند و بردارهای هم سنگ یا مساوی گویند.
جابه جایی:
جابه جایی یک جسم، پاره خط جهت داری است که ابتدای آن مکان آغازی و انتهای آن مکان پایانی جسم و طول آن مقدار تغییر مکان است. دو جابه جایی را وقتی برابر می گویند که به یک اندازه و در یک جهت (هم راستا و هم سو) باشند.
جمع بردارهای جابه جایی
حاصل جمع دو یا چند برادر را برآیند آن بردارها (یا بردار برآیند) می نامند. برای یافتن برآیند دو بردارa و bمی توانیم از یک نقطه دو بردار برابرa و bرسم کنیم. بردار برآیند قطر متوازی الاضلاعی است که نقطه شروع دو بردار را به رأس مقابل وصل می کند. (قاعده متوازی الاضلاع برای جمع بردارها)
نکته: بردار برآیند از رابطه ی زیر نیز به دست می آید.
مثال: بردار برآیند بردارهای a و bو c را به دست آورید.
پاسخ: بردارهای مساویa و bو c را پشت هم رسم می کنیم و ابتدای بردار اول را به انتهای بردار آخر وصل می کنیم.
نکته: اگر دو بردار a و b بر هم عمود باشند. بزرگی بردار برآیند (R) از رابطه زیر به دست می آید:
R = √(a[SUP]2[/SUP] + b[SUP]2[/SUP])
حاصل ضرب یک عدد در یک بردار
هر گاه عدد m را در یک بردار ضرب کنیم، بزرگی بردار حاصل m برابر بردار اول است.
جهت بردار حاصل ضرب با بردار اولیه یکی است ® 0 >m
بردار حاصل ضرب در خلاف جهت بردار اولیه است ® 0<m
(یعنی وقتی برداری را در یک عدد مثبت ضرب می کنیم فقط بزرگی آن تغییر می کند؛ ولی وقتی در یک عدد منفی ضرب می کنیم جهت آن نیز تغییر می کند.)
تفریق دو بردار
حاصل تفریق دو بردار نیز یک بردار است. برای تفریق دو بردار ابتدا از یک نقطه به عنوان مبدأ، دو بردار a و bرا رسم می کنیم. بردار c حاصل تفریق بردارهای a و bاست و راستای c انتها بردارهای a و bرا به هم وصل می کند.
جابه جایی:
جابه جایی یک جسم، پاره خط جهت داری است که ابتدای آن مکان آغازی و انتهای آن مکان پایانی جسم و طول آن مقدار تغییر مکان است. دو جابه جایی را وقتی برابر می گویند که به یک اندازه و در یک جهت (هم راستا و هم سو) باشند.
جمع بردارهای جابه جایی
حاصل جمع دو یا چند برادر را برآیند آن بردارها (یا بردار برآیند) می نامند. برای یافتن برآیند دو بردارa و bمی توانیم از یک نقطه دو بردار برابرa و bرسم کنیم. بردار برآیند قطر متوازی الاضلاعی است که نقطه شروع دو بردار را به رأس مقابل وصل می کند. (قاعده متوازی الاضلاع برای جمع بردارها)
R = √(a2 + b2 + 2abcos)
جمع برداری خاصیت جابه جایی دارد یعنی به ترتیب بردارها بستگی ندارد. یک روش دیگر برای جمع دو یا چند بردار این است که از انتهای بردار اول برداری مساوی بردار دوم و از انتهای بردار دوم برداری مساوی بردار سوم و همین طور تا آخر رسم کنیم. بردار برآیند برداری است که ابتدای آن ابتدای بردار اول و انتهای آن انتهای بردار آخر باشد.
مثال: بردار برآیند بردارهای a و bو c را به دست آورید.
پاسخ: بردارهای مساویa و bو c را پشت هم رسم می کنیم و ابتدای بردار اول را به انتهای بردار آخر وصل می کنیم.
نکته: اگر دو بردار a و b بر هم عمود باشند. بزرگی بردار برآیند (R) از رابطه زیر به دست می آید:
R = √(a[SUP]2[/SUP] + b[SUP]2[/SUP])
حاصل ضرب یک عدد در یک بردار
هر گاه عدد m را در یک بردار ضرب کنیم، بزرگی بردار حاصل m برابر بردار اول است.
جهت بردار حاصل ضرب با بردار اولیه یکی است ® 0 >m
بردار حاصل ضرب در خلاف جهت بردار اولیه است ® 0<m
(یعنی وقتی برداری را در یک عدد مثبت ضرب می کنیم فقط بزرگی آن تغییر می کند؛ ولی وقتی در یک عدد منفی ضرب می کنیم جهت آن نیز تغییر می کند.)
تفریق دو بردار
حاصل تفریق دو بردار نیز یک بردار است. برای تفریق دو بردار ابتدا از یک نقطه به عنوان مبدأ، دو بردار a و bرا رسم می کنیم. بردار c حاصل تفریق بردارهای a و bاست و راستای c انتها بردارهای a و bرا به هم وصل می کند.
نکات مهم بردارها
نکات مهم بردارها
نکته ۱ -کمیتهایی که دارای اندازه و جهت باشند ، کمیت برداری نامیده می شوند .مانند نیرو ، سرعت ، جابجایی و اندازه حرکت
نکته ۲ - برای جمع دو بردار از روش متوازی الاضلاع یا مثلث استفاده می کنیم . در روش متوازی الاضلاع دو بردار را از یک نقطه رسم می کنیم و از انتهای هر یک خطی موازی دیگری رسم می کنیم تا یکدیگر را قطع کنند در این حالت برداری که مبدا را به محل تقاطع وصل می کند برآیند دو بردار می باشد.
نکته ۳ - طول هر بردار را بزرگی آن می نامیم و از رابطه زیر محاسبه می شود .
[SUP]۲/۱[/SUP] ( R=( A[SUP]2[/SUP]+ B[SUP]2[/SUP]+2A.B.cosΘ
در این رابطه A و B طول دو بردار و Θ زاویه میان دو بردار است .
نکته ۴ - هر بردار را می توان بر حسب تصاویر ( مولفه ) آن بر روی محورها تجزیه نمود .اگر Θ زاویه آن بردار با محور X باشد داریم :
A=A[SUB]x[/SUB]i+A[SUB]y[/SUB]j
در این رابطه A[SUB]x[/SUB] و A[SUB]y[/SUB] تصاویر ( مولفه ) بردار بر روی محورهای X و Y است و داریم:
A[SUB]x[/SUB]=AcosΘ
A[SUB]y[/SUB]=AsinΘ
نکته ۵ - بزرگی هر بردار از رابطه زیر بدست می آید :
اAا = A[SUB]x[/SUB][SUP]2[/SUP]+A[SUB]y[/SUB][SUP]2[/SUP])[SUP]1/2 [/SUP])
نکته ۶ - اگر دو بردار باهم مساوی باشند برآیند آنها از رابطه زیر محاسبه می شود :
R=2AcosΘ/2
نکته ۷ - اگر طول دو بردار مساوی باشد و زاویه میان انها ۹۰ درجه باشد بزرگی برآیند آنها برابر Γ۲ برابر یکی از آنها است .
نکته ۸ - اگر طول دو بردار مساوی باشد و زاویه میان آنها ۱۲۰ درجه باشد . بزرگی برآیند آنها برابر طول یکی از بردارها است .
نکته ۹ - اگر زاویه میان دو بردار با طول مساوی برابر ۶۰ درجه باشد بزرگی برآیند آنها Γ۳ برابر طول یکی از بردارها است .
نکته ۱۰ - برای بدست آوردن تفاضل دو بردار ، بردار اول را با قرینه بردار دوم جمع می کنیم .
نکته ۱۱ - برای بدست آوردن بزرگی تفاضل دو بردار ، در رابطه جمع بجای Θ زاویه Π-Θ قرار می دهیم . جهت بردار تفاضل در جهت قطر دیگر متوازی الاضلاع است .
نکات مهم بردارها
نکته ۱ -کمیتهایی که دارای اندازه و جهت باشند ، کمیت برداری نامیده می شوند .مانند نیرو ، سرعت ، جابجایی و اندازه حرکت
نکته ۲ - برای جمع دو بردار از روش متوازی الاضلاع یا مثلث استفاده می کنیم . در روش متوازی الاضلاع دو بردار را از یک نقطه رسم می کنیم و از انتهای هر یک خطی موازی دیگری رسم می کنیم تا یکدیگر را قطع کنند در این حالت برداری که مبدا را به محل تقاطع وصل می کند برآیند دو بردار می باشد.
نکته ۳ - طول هر بردار را بزرگی آن می نامیم و از رابطه زیر محاسبه می شود .
[SUP]۲/۱[/SUP] ( R=( A[SUP]2[/SUP]+ B[SUP]2[/SUP]+2A.B.cosΘ
در این رابطه A و B طول دو بردار و Θ زاویه میان دو بردار است .
نکته ۴ - هر بردار را می توان بر حسب تصاویر ( مولفه ) آن بر روی محورها تجزیه نمود .اگر Θ زاویه آن بردار با محور X باشد داریم :
A=A[SUB]x[/SUB]i+A[SUB]y[/SUB]j
در این رابطه A[SUB]x[/SUB] و A[SUB]y[/SUB] تصاویر ( مولفه ) بردار بر روی محورهای X و Y است و داریم:
A[SUB]x[/SUB]=AcosΘ
A[SUB]y[/SUB]=AsinΘ
نکته ۵ - بزرگی هر بردار از رابطه زیر بدست می آید :
اAا = A[SUB]x[/SUB][SUP]2[/SUP]+A[SUB]y[/SUB][SUP]2[/SUP])[SUP]1/2 [/SUP])
نکته ۶ - اگر دو بردار باهم مساوی باشند برآیند آنها از رابطه زیر محاسبه می شود :
R=2AcosΘ/2
نکته ۷ - اگر طول دو بردار مساوی باشد و زاویه میان انها ۹۰ درجه باشد بزرگی برآیند آنها برابر Γ۲ برابر یکی از آنها است .
نکته ۸ - اگر طول دو بردار مساوی باشد و زاویه میان آنها ۱۲۰ درجه باشد . بزرگی برآیند آنها برابر طول یکی از بردارها است .
نکته ۹ - اگر زاویه میان دو بردار با طول مساوی برابر ۶۰ درجه باشد بزرگی برآیند آنها Γ۳ برابر طول یکی از بردارها است .
نکته ۱۰ - برای بدست آوردن تفاضل دو بردار ، بردار اول را با قرینه بردار دوم جمع می کنیم .
نکته ۱۱ - برای بدست آوردن بزرگی تفاضل دو بردار ، در رابطه جمع بجای Θ زاویه Π-Θ قرار می دهیم . جهت بردار تفاضل در جهت قطر دیگر متوازی الاضلاع است .
براي بررسي حرکت يک جسم ابتدا به تعريف چند کميت مي پردازيم.
بردار مکان و بردار جابه جايي
بردار مکان موقعيت مکاني جسم را در صفحه مختصات نشان مي دهد. ابتداي بردار مکان بعداً مختصات و انتهاي آن نقطه اي است که جسم در آن واقع شده است.
فرض کنيد که يک جسم متحرک در لحظه t[SUB]1[/SUB] در نقطه A باشد و در لحظه t[SUB]2[/SUB] به نقطه B رسيده باشد. بردار جابه جايي بين دو لحظه t[SUB]1[/SUB] و t[SUB]2[/SUB] برداري است که ابتداي آن مکان متحرک در لحظه t[SUP]1[/SUP] و انتهاب آن مکان متحرک در لحظه t[SUB]2[/SUB] باشد.
Δr تفاضل r[SUB]2[/SUB] و r[SUB]1[/SUB] است يعني r[SUB]2[/SUB]-r[SUB]1[/SUB] = Δr
بردار جابه جاهايي به مسير حرکت بستگي ندارد و فقط با داشتن دو نقطه (مکان جسم در لحظه t1 و مکان جسم در لحظه t[SUB]2[/SUB]) رسم مي شود.
حرکت روي خط راست
هر گاه راستاي حرکت جسم متحرک، يک خط راست باشد در تمام لحظه ها بردار جابه جايي هايي متحرک بر همان راستا خواهد بود. مبدأ هم روي همين راستا انتخاب مي شود در اين صورت محاسبه بر روي اين بردارها به سادگي انجام مي گيرد.
نمودار مکان – زمان
اين نمودار مکان جسم را در زمانهاي مختلف نشان مي دهد. غالباً محور افقي زمان و محور قائم مکان جسم را نشان مي دهد. با استفاده از اين نمودار مي توان دريافت که متحرک در هر لحظه در چه مکاني قرار دارد و جابه جايي آن بين هر دو لحظه چقدر است.
سرعت متوسط و تعيين آن به کمک نمودار مکان - زمان
تغيير مکان يک جسم تقسيم بر تغييرات زمان را سرعت متوسط مي گويند. سرعت متوسط به صورت v نشان داده مي شود. سرعت متوسط کميتي برداري است که با بردار جابه جايي هم جهت است. يکاي سرعت متوسط متر بر ثانيه (m/s) مي باشد.
نمودار مکان . زمان يک جسم متحرک نشان داده شده است. سرعت متوسط بين دو نقطه A و
بردار مکان و بردار جابه جايي
بردار مکان موقعيت مکاني جسم را در صفحه مختصات نشان مي دهد. ابتداي بردار مکان بعداً مختصات و انتهاي آن نقطه اي است که جسم در آن واقع شده است.
فرض کنيد که يک جسم متحرک در لحظه t[SUB]1[/SUB] در نقطه A باشد و در لحظه t[SUB]2[/SUB] به نقطه B رسيده باشد. بردار جابه جايي بين دو لحظه t[SUB]1[/SUB] و t[SUB]2[/SUB] برداري است که ابتداي آن مکان متحرک در لحظه t[SUP]1[/SUP] و انتهاب آن مکان متحرک در لحظه t[SUB]2[/SUB] باشد.
Δr تفاضل r[SUB]2[/SUB] و r[SUB]1[/SUB] است يعني r[SUB]2[/SUB]-r[SUB]1[/SUB] = Δr
بردار جابه جاهايي به مسير حرکت بستگي ندارد و فقط با داشتن دو نقطه (مکان جسم در لحظه t1 و مکان جسم در لحظه t[SUB]2[/SUB]) رسم مي شود.
حرکت روي خط راست
هر گاه راستاي حرکت جسم متحرک، يک خط راست باشد در تمام لحظه ها بردار جابه جايي هايي متحرک بر همان راستا خواهد بود. مبدأ هم روي همين راستا انتخاب مي شود در اين صورت محاسبه بر روي اين بردارها به سادگي انجام مي گيرد.
نمودار مکان – زمان
اين نمودار مکان جسم را در زمانهاي مختلف نشان مي دهد. غالباً محور افقي زمان و محور قائم مکان جسم را نشان مي دهد. با استفاده از اين نمودار مي توان دريافت که متحرک در هر لحظه در چه مکاني قرار دارد و جابه جايي آن بين هر دو لحظه چقدر است.
سرعت متوسط و تعيين آن به کمک نمودار مکان - زمان
تغيير مکان يک جسم تقسيم بر تغييرات زمان را سرعت متوسط مي گويند. سرعت متوسط به صورت v نشان داده مي شود. سرعت متوسط کميتي برداري است که با بردار جابه جايي هم جهت است. يکاي سرعت متوسط متر بر ثانيه (m/s) مي باشد.
| Δx Δt | = | جابه جايي زماني که جابه جايي رخ داده | V= |
نمودار مکان . زمان يک جسم متحرک نشان داده شده است. سرعت متوسط بين دو نقطه A و
| B مساوي است با | همان شيب خط AB است. |
بررسی حرکت دو بعدی
بررسی حرکت دو بعدی
حرکت در دو بعد یکی از عام ترین حرکت هایی است که به طور روز مره با آن مواجه می شویم. حرکت یک اتومبیل در یک پیچ و یا حرکت یک گلوله پس از شلیک و یا رها شدن یک تیر از کمان از نمونه مثال هایی است که می توان از حرکت در دو بعد نام برد.
به طور کلی، حرکت در دو بعد ترکیبی از دو حرکت یک بعدی در دو راستای متفاوت x و y می باشد. در این جا می خواهیم با صرف نظر کردن از نیروی اصطکاک فضایی که متحرک در آن حرکت می کند، را بررسی می کنیم.
حرکت پرتابه از دو نوع حرکت در راستای افقی و عمودی تشکیل شده است:
1 ) حرکت افقی حرکتی با شتاب صفر و با سرعت ثابت می باشد.
2 ) حرکت عمودی حرکتی با شتاب g - و در راستای عمودی است.
با توجه به شکل زیر می توانیم بردار سرعت و شتاب را به صورت زیر بنویسیم:
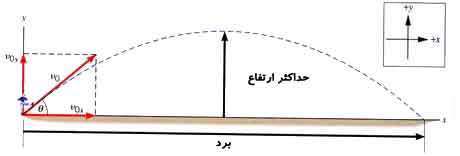
دقت داشته باشید که بردار رسم شده، بردار سرعت اولیه می باشد و زاویه نمایش داده شده، زاویه پرتاب اولیه می باشد، آن گاه خواهیم داشت :
معادله x ، معادله مکان بر حسب زمان پرتابه در راستای افقی می باشد و معادله y ، مکان متحرک در زمان های مختلف می باشد، در معادله x، مقدار t را به دست آورید و مقدار به دست آمده را در معادله y قرار دهید. مبدأ مکان و زمان را روی صفر قرار دهید (t[SUB]0[/SUB]=0 و x[SUB]0[/SUB] = y[SUB]0[/SUB] = 0)
معادله y بر حسب x به صورت یک منحنی سهمی خواهد بود که تقعر منفی دارد.
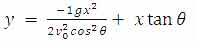[h=2]برد پرتابه
[/h]مقدار بیشینه فاصله جسم از نقطه پرتاب را برد پرتابه می گویند و با R نمایش می دهند، اگر متحرک در طی مسیر، در یک سطح هم تراز برگردد، می توان با صفر قرار دادن مقدار y در معادله فوق مقدار R را به صورت زیر به دست آورد:
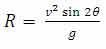
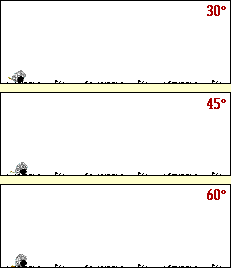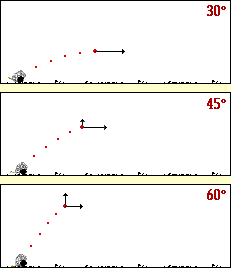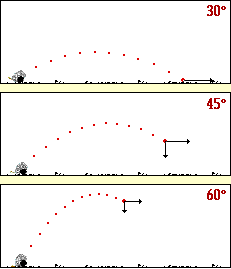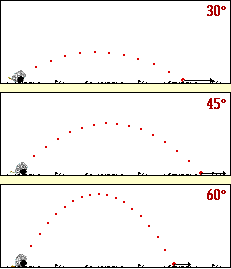
برای بررسی حدستان، می توانید به این شیوه عمل نمایید: تابع سینوس، تابعی است که برد آن در بازه [1 , 1- ] ، قرار دارد، با توجه به فرمول برد پرتابه، وقتی این مقدار بیشینه می شود که مقدار تابع سینوس یک شود، و این موقعیت وقتی روی می دهد که زاویه اولیه پرتاب 45 درجه باشد.
یادآوری: برد پرتابه تحت زاویه 45 درجه به بیشترین مقدار خود می رسد.
[h=2]ارتفاع اوج
[/h]بالاترین ارتفاعی را که یک پرتابه به آن می رسد، ارتفاع اوج نام دارد. در این جا برای یافتن ارتفاع اوج، مراحل زیر را انجام دهید:
1) مشتق y را نسبت به x بگیرید.
2) مقدار مشتق را برابر صفر قرار دهید.
3) مقدار x به دست آمده از فرمول بالا را دوباره در معادله y قرار دهید و جواب را ساده کنید.
در پایان، پس از انجام مراحل فوق مقدار H، یعنی مقدار ارتفاع اوج در حرکت پرتابه به صورت زیر به دست خواهد آمد:
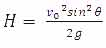شایان ذکر است که در نقطه اوج، مولفه عمودی، سرعت صفر است. بنابراین سرعت ذره در نقطه اوج برابر است با :
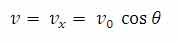
بررسی حرکت دو بعدی
حرکت در دو بعد یکی از عام ترین حرکت هایی است که به طور روز مره با آن مواجه می شویم. حرکت یک اتومبیل در یک پیچ و یا حرکت یک گلوله پس از شلیک و یا رها شدن یک تیر از کمان از نمونه مثال هایی است که می توان از حرکت در دو بعد نام برد.
به طور کلی، حرکت در دو بعد ترکیبی از دو حرکت یک بعدی در دو راستای متفاوت x و y می باشد. در این جا می خواهیم با صرف نظر کردن از نیروی اصطکاک فضایی که متحرک در آن حرکت می کند، را بررسی می کنیم.
حرکت پرتابه از دو نوع حرکت در راستای افقی و عمودی تشکیل شده است:
1 ) حرکت افقی حرکتی با شتاب صفر و با سرعت ثابت می باشد.
2 ) حرکت عمودی حرکتی با شتاب g - و در راستای عمودی است.
با توجه به شکل زیر می توانیم بردار سرعت و شتاب را به صورت زیر بنویسیم:
دقت داشته باشید که بردار رسم شده، بردار سرعت اولیه می باشد و زاویه نمایش داده شده، زاویه پرتاب اولیه می باشد، آن گاه خواهیم داشت :
معادله y بر حسب x به صورت یک منحنی سهمی خواهد بود که تقعر منفی دارد.
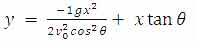
[/h]مقدار بیشینه فاصله جسم از نقطه پرتاب را برد پرتابه می گویند و با R نمایش می دهند، اگر متحرک در طی مسیر، در یک سطح هم تراز برگردد، می توان با صفر قرار دادن مقدار y در معادله فوق مقدار R را به صورت زیر به دست آورد:
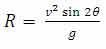
با توجه به شکل زیر آیا می توانید حدس بزنید که برد پرتابه تحت چه زاویه ای مقدار برد پرتابه بیشینه می شود؟
برای بررسی حدستان، می توانید به این شیوه عمل نمایید: تابع سینوس، تابعی است که برد آن در بازه [1 , 1- ] ، قرار دارد، با توجه به فرمول برد پرتابه، وقتی این مقدار بیشینه می شود که مقدار تابع سینوس یک شود، و این موقعیت وقتی روی می دهد که زاویه اولیه پرتاب 45 درجه باشد.
یادآوری: برد پرتابه تحت زاویه 45 درجه به بیشترین مقدار خود می رسد.
[h=2]ارتفاع اوج
[/h]بالاترین ارتفاعی را که یک پرتابه به آن می رسد، ارتفاع اوج نام دارد. در این جا برای یافتن ارتفاع اوج، مراحل زیر را انجام دهید:
1) مشتق y را نسبت به x بگیرید.
2) مقدار مشتق را برابر صفر قرار دهید.
3) مقدار x به دست آمده از فرمول بالا را دوباره در معادله y قرار دهید و جواب را ساده کنید.
در پایان، پس از انجام مراحل فوق مقدار H، یعنی مقدار ارتفاع اوج در حرکت پرتابه به صورت زیر به دست خواهد آمد:
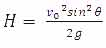
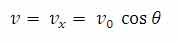
سرعت موج طولی زیمانسکی
سرعت موج طولی زیمانسکی
سلام
میشه برام اثبات فرمول زیر رو بنویسید؟
زیمانسکی سرعت موج طولی را مطابق شکل زیر به دست آورد. پیستونی هوای درون سیلندر با سرعت w0 متراکم میکند و جبهه ی موج متراکم شده با سرعت ثابت W به جلو می رود.
نشان دهید سرعت موج طولیW از رابطه ی زیر به دست می آید:
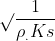
سرعت موج طولی زیمانسکی
سلام
میشه برام اثبات فرمول زیر رو بنویسید؟
زیمانسکی سرعت موج طولی را مطابق شکل زیر به دست آورد. پیستونی هوای درون سیلندر با سرعت w0 متراکم میکند و جبهه ی موج متراکم شده با سرعت ثابت W به جلو می رود.
نشان دهید سرعت موج طولیW از رابطه ی زیر به دست می آید:
این اثباته....
اگه میشه کسی از روی حل برام توضیح بده....
اگه میشه کسی از روی حل برام توضیح بده....
آخرین ویرایش:
ادامه ی اثبات
ادامه ی اثبات
ادامه ی اثبات
Similar threads
| Thread starter | عنوان | تالار | پاسخ ها | تاریخ |
|---|---|---|---|---|
|
تجديد آزمايش سرعت نوترينوها/ تلاش براي اثبات يا رد سرعت بالاتر از نور در ذرات بنيادين | فیزیک | 0 | |
| R | کمک: چطور می شه اثبات کرد که ضریب انبساط سطحی دوبرابر ضریب انبساط طولی است؟ | فیزیک | 2 | |
|
دقیق ترین اثبات نسبیت اینیشتین. | فیزیک | 0 | |
|
اثبات قانون گاوس | فیزیک | 4 |
Similar threads
-
تجديد آزمايش سرعت نوترينوها/ تلاش براي اثبات يا رد سرعت بالاتر از نور در ذرات بنيادين
- شروع شده توسط Mohsen 89
- پاسخ ها: 0
-
کمک: چطور می شه اثبات کرد که ضریب انبساط سطحی دوبرابر ضریب انبساط طولی است؟
- شروع شده توسط raika_sorena
- پاسخ ها: 2
-
-